In mathematics and probability theory, Skorokhod's embedding theorem is either or both of two theorems that allow one to regard any suitable collection of random variables as a Wiener process (Brownian motion) evaluated at a collection of stopping times. Both results are named for the Ukrainian mathematician A. V. Skorokhod.
Let X be a real-valued random variable with expected value 0 and finite variance; let W denote a canonical real-valued Wiener process. Then there is a stopping time (with respect to the natural filtration of W), τ, such that Wτ has the same distribution as X,
and
Let X1, X2, ... be a sequence of independent and identically distributed random variables, each with expected value 0 and finite variance, and let
Then there is a sequence of stopping times τ1≤τ2≤ ... such that the have the same joint distributions as the partial sums Sn and τ1, τ2−τ1, τ3−τ2, ... are independent and identically distributed random variables satisfying
and
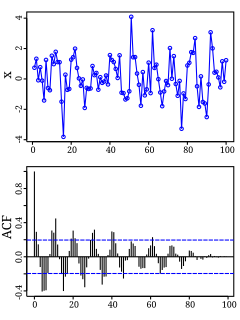
Autocorrelation, also known as serial correlation, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals.
In probability theory, the expected value of a random variable is a key aspect of its probability distribution. The expected value of a discrete random variable is the probability-weighted average of all its possible values. In other words, each possible value the random variable can assume is multiplied by its probability of occurring, and the resulting products are summed to produce the expected value. Intuitively, a random variable's expected value represents the mean of a large number of independent realizations of the random variable. The expected value of a probability distribution is also known as the expectation, mathematical expectation, mean, average, or first moment.
In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes. The same concepts are known in more general mathematics as stochastic convergence and they formalize the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behavior that is essentially unchanging when items far enough into the sequence are studied. The different possible notions of convergence relate to how such a behavior can be characterized: two readily understood behaviors are that the sequence eventually takes a constant value, and that values in the sequence continue to change but can be described by an unchanging probability distribution.
In mathematics, the Wiener process is a real valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.
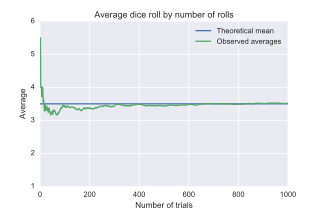
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and will tend to become closer to the expected value as more trials are performed.
In probability theory, a martingale is a sequence of random variables for which, at a particular time, the conditional expectation of the next value in the sequence, given all prior values, is equal to the present value.
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy.
In probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”: a random variable whose value is interpreted as the time at which a given stochastic process exhibits a certain behavior of interest. A stopping time is often defined by a stopping rule, a mechanism for deciding whether to continue or stop a process on the basis of the present position and past events, and which will almost always lead to a decision to stop at some finite time.
In probability theory, Wald's equation, Wald's identity or Wald's lemma is an important identity that simplifies the calculation of the expected value of the sum of a random number of random quantities. In its simplest form, it relates the expectation of a sum of randomly many finite-mean, independent and identically distributed random variables to the expected number of terms in the sum and the random variables' common expectation under the condition that the number of terms in the sum is independent of the summands.
In probability theory, the central limit theorem says that, under certain conditions, the sum of many independent identically-distributed random variables, when scaled appropriately, converges in distribution to a standard normal distribution. The martingale central limit theorem generalizes this result for random variables to martingales, which are stochastic processes where the change in the value of the process from time t to time t + 1 has expectation zero, even conditioned on previous outcomes.
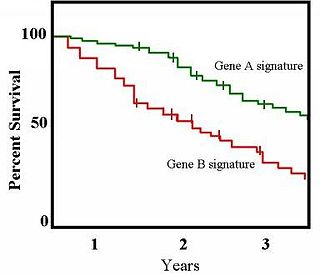
The Kaplan–Meier estimator, also known as the product limit estimator, is a non-parametric statistic used to estimate the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In other fields, Kaplan–Meier estimators may be used to measure the length of time people remain unemployed after a job loss, the time-to-failure of machine parts, or how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier, who each submitted similar manuscripts to the Journal of the American Statistical Association. The journal editor, John Tukey, convinced them to combine their work into one paper, which has been cited about 57,000 times since its publication.
In probability theory, Donsker's theorem, named after Monroe D. Donsker, is a functional extension of the central limit theorem.
In statistics, an exchangeable sequence of random variables is a sequence X1, X2, X3, ... whose joint probability distribution does not change when the positions in the sequence in which finitely many of them appear are altered. Thus, for example the sequences
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales. The definition used in measure theory is closely related to, but not identical to, the definition typically used in probability.
In probability theory, the optional stopping theorem says that, under certain conditions, the expected value of a martingale at a stopping time is equal to its initial expected value. Since martingales can be used to model the wealth of a gambler participating in a fair game, the optional stopping theorem says that, on average, nothing can be gained by stopping play based on the information obtainable so far. Certain conditions are necessary for this result to hold true. In particular, the theorem applies to doubling strategies.
In probability theory, Lindeberg's condition is a sufficient condition for the central limit theorem (CLT) to hold for a sequence of independent random variables. Unlike the classical CLT, which requires that the random variables in question have finite variance and be both independent and identically distributed, Lindeberg's CLT only requires that they have finite variance, satisfy Lindeberg's condition, and be independent. It is named after the Finnish mathematician Jarl Waldemar Lindeberg.
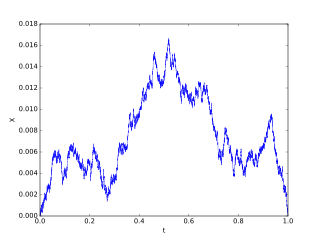
In probability theory a Brownian excursion process is a stochastic process that is closely related to a Wiener process. Realisations of Brownian excursion processes are essentially just realizations of a Wiener process selected to satisfy certain conditions. In particular, a Brownian excursion process is a Wiener process conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive. BEPs are important because, among other reasons, they naturally arise as the limit process of a number of conditional functional central limit theorems.
In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. This property is usually abbreviated as i.i.d. or iid or IID. Herein, i.i.d. is used, because it is the most prevalent.
