
In physics and mathematics, the dimension of a mathematical space is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one (1D) because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface such as a plane or the surface of a cylinder or sphere has a dimension of two (2D) because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object can always be rotated about an infinite number of imaginary lines called rotation axes. If the axis passes through the body's center of mass, the body is said to rotate upon itself, or spin. A rotation around an external point, e.g. the planet Earth around the Sun, is called a revolution or orbital revolution, typically when it is produced by gravity. The axis is called a pole.

The semicircular canals or semicircular ducts are three semicircular, interconnected tubes located in the innermost part of each ear, the inner ear. The three canals are the horizontal, superior and posterior semicircular canals.
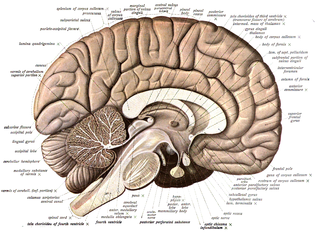
Neuroanatomy is the study of the structure and organization of the nervous system. In contrast to animals with radial symmetry, whose nervous system consists of a distributed network of cells, animals with bilateral symmetry have segregated, defined nervous systems. Their neuroanatomy is therefore better understood. In vertebrates, the nervous system is segregated into the internal structure of the brain and spinal cord and the routes of the nerves that connect to the rest of the body. The delineation of distinct structures and regions of the nervous system has been critical in investigating how it works. For example, much of what neuroscientists have learned comes from observing how damage or "lesions" to specific brain areas affects behavior or other neural functions.

In mathematics, a frieze or frieze pattern is a design on a two-dimensional surface that is repetitive in one direction. Such patterns occur frequently in architecture and decorative art. A frieze group is the set of symmetries of a frieze pattern, specifically the set of isometries of the pattern, that is geometric transformations built from rigid motions and reflections that preserve the pattern. The mathematical study of frieze patterns reveals that they can be classified into seven types according to their symmetries.

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles and tiles as well as wallpaper.

Rudolf von Laban, also known as Rudolf Laban, was an Austro-Hungarian dance artist and theorist. He is considered as one of the pioneers of modern dance in Europe as the "Founding Father of the Expressionist Dance" in Germany. His work laid the foundations for Laban Movement Analysis, Labanotation, other more specific developments in dance notation and the evolution of many varieties of Laban movement analysis. He is considered to be one of the most important figures in the history of dance.

Labanotation or Kinetography Laban is a notation system for recording and analyzing human movement that was derived from the work of Rudolf Laban who described it in Schrifttanz in 1928. His initial work has been further developed by Ann Hutchinson Guest and others, and is used as a type of dance notation in other applications including Laban Movement Analysis, robotics and human movement simulation.
Laban movement analysis (LMA), sometimes Laban/Bartenieff movement analysis, is a method and language for describing, visualizing, interpreting and documenting human movement. It is based on the original work of Rudolf Laban, which was developed and extended by Lisa Ullmann, Irmgard Bartenieff, Warren Lamb and others. LMA draws from multiple fields including anatomy, kinesiology and psychology. It is used by dancers, actors, musicians and athletes; by health professionals such as physical and occupational therapists and psychotherapists; and in anthropology, business consulting and leadership development.
Bartenieff Fundamentals are a set of principles for "corrective body movement" developed by Irmgard Bartenieff, who studied with Rudolf Laban and colleagues in Germany (1925). After coming to the United States in the 1940s and becoming a physical therapist, Bartenieff developed the method in the form of a set of exercises, based on concepts and principles of kinesiological functioning, that can be extended into all types of movement possibilities. Bartenieff in developing this work fused her studies in both Laban movement analysis with Physiotherapeutic principles and the influence of both is a strong component of the Fundamentals.
The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn.
Groundwater models are computer models of groundwater flow systems, and are used by hydrogeologists. Groundwater models are used to simulate and predict aquifer conditions.

An architectural drawing or architect's drawing is a technical drawing of a building that falls within the definition of architecture. Architectural drawings are used by architects and others for a number of purposes: to develop a design idea into a coherent proposal, to communicate ideas and concepts, to convince clients of the merits of a design, to assist a building contractor to construct it based on design intent, as a record of the design and planned development, or to make a record of a building that already exists.

Warren Lamb was a British management consultant and pioneer in the field of nonverbal behavior. After studying with Rudolf Laban he developed Movement Pattern Analysis - a system for analysing and interpreting movement behaviour, which has been applied in numerous fields including management consulting, executive recruitment and therapy. Lamb used the MPA system in advising multinational corporations, typically at top team level, and also government organizations. Lamb differentiated his system from the popular body language literature and argued that the key to interpreting behaviour was not fixed gestures but the dynamics of movement. Lamb's underlying theory was that each individual has a unique way of moving which is constant and that these distinct movement patterns reflect the individual's way of thinking and behaving. In MPA he developed a system for identifying these patterns and relating them to behaviours, with the aim of predicting how people will behave in various situations based on their movement patterns. Recent studies led by Harvard University and Brown University in the United States reported significant predictive reliability for the system.

An anatomical plane is a hypothetical plane used to transect the body, in order to describe the location of structures or the direction of movements. In human and animal anatomy, three principal planes are used:
Laban Notation Symbols generally refers to the wide range of notation symbols developing from the original work of Rudolf Laban and used in many different types of Laban Movement Study such as Labanotation and Laban Movement Analysis for graphically representing human body positions and movements.

Strip photography is a photographic technique of capturing a 2-dimensional image as a sequence of 1-dimensional images over time, rather than a single 2-dimensional at one point in time. As one moves across, one moves in time in addition to moving in space. The image can be loosely interpreted as a collection of thin vertical or horizontal strips patched together, hence the name. This is correct if the strips are discrete, as in a digital sensor that captures one line at a time, but in film photography, the image is produced continuously, and thus the "strips" are infinitesimal – a smooth gradation.
In astronomy, geography, and related sciences and contexts, a direction or plane passing by a given point is said to be vertical if it contains the local gravity direction at that point. Conversely, a direction or plane is said to be horizontal if it is perpendicular to the vertical direction. In general, something that is vertical can be drawn from up to down, such as the y-axis in the Cartesian coordinate system.

Irmgard Bartenieff was a dance theorist, dancer, choreographer, physical therapist, and a leading pioneer of dance therapy. A student of Rudolf Laban, she pursued cross-cultural dance analysis, and generated a new vision of possibilities for human movement and movement training. From her experiences applying Laban’s concepts of dynamism, three-dimensional movement and mobilization to the rehabilitation of people affected by polio in the 1940s, she went on to develop her own set of movement methods and exercises, known as Bartenieff Fundamentals.



















