Spectral radiance

Last updated April 22, 2024

In radiometry, spectral radiance or specific intensity is the radiance of a surface per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. The SI unit of spectral radiance in frequency is the watt per steradian per square metre per hertz (W·sr⁻¹·m⁻²·Hz⁻¹) and that of spectral radiance in wavelength is the watt per steradian per square metre per metre (W·sr⁻¹·m⁻³)—commonly the watt per steradian per square metre per nanometre (W·sr⁻¹·m⁻²·nm⁻¹). The microflick is also used to measure spectral radiance in some fields.^[1]^[2]

Spectral radiance gives a full radiometric description of the field of classical electromagnetic radiation of any kind, including thermal radiation and light. It is conceptually distinct from the descriptions in explicit terms of Maxwellian electromagnetic fields or of photon distribution. It refers to material physics as distinct from psychophysics.

For the concept of specific intensity, the line of propagation of radiation lies in a semi-transparent medium which varies continuously in its optical properties. The concept refers to an area, projected from the element of source area into a plane at right angles to the line of propagation, and to an element of solid angle subtended by the detector at the element of source area.^[3]^[4]^[5]^[6]^[7]^[8]^[9]

The term brightness is also sometimes used for this concept.^[3]^[10] The SI system states that the word brightness should not be so used, but should instead refer only to psychophysics.

Definition

The specific (radiative) intensity is a quantity that describes the rate of radiative transfer of energy at $P 1$ , a point of space with coordinates $x$ , at time $t$ . It is a scalar-valued function of four variables, customarily^[3]^[4]^[5]^[11]^[12]^[13] written as

I(\mathbf {x} ,t;\mathbf {r} _{1},\nu )

where:

$ν$ denotes frequency.
$r 1$ denotes a unit vector, with the direction and sense of the geometrical vector $r$ in the line of propagation from
the effective source point $P 1$ , to
a detection point $P 2$ .

$I (x, t; r 1, ν)$ is defined to be such that a virtual source area, $dA 1$ , containing the point $P 1$ , is an apparent emitter of a small but finite amount of energy $dE$ transported by radiation of frequencies $(ν, ν + dν)$ in a small time duration $d t$ , where

dE=I(\mathbf {x} ,t;\mathbf {r} _{1},\nu )\cos(\theta _{1})\,dA_{1}\,d\Omega _{1}\,d\nu \,dt\,,

and where $θ 1$ is the angle between the line of propagation $r$ and the normal $P 1 N 1$ to $dA 1$ ; the effective destination of $dE$ is a finite small area $dA 2$ , containing the point $P 2$ , that defines a finite small solid angle $d Ω 1$ about $P 1$ in the direction of $r$ . The cosine accounts for the projection of the source area $dA 1$ into a plane at right angles to the line of propagation indicated by $r$ .

The use of the differential notation for areas $dA i$ indicates they are very small compared to $r 2$ , the square of the magnitude of vector $r$ , and thus the solid angles $d Ω i$ are also small.

There is no radiation that is attributed to $P 1$ itself as its source, because $P 1$ is a geometrical point with no magnitude. A finite area is needed to emit a finite amount of light.

Invariance

For propagation of light in a vacuum, the definition of specific (radiative) intensity implicitly allows for the inverse square law of radiative propagation.^[12]^[14] The concept of specific (radiative) intensity of a source at the point $P 1$ presumes that the destination detector at the point $P 2$ has optical devices (telescopic lenses and so forth) that can resolve the details of the source area $dA 1$ . Then the specific radiative intensity of the source is independent of the distance from source to detector; it is a property of the source alone. This is because it is defined per unit solid angle, the definition of which refers to the area $d A 2$ of the detecting surface.

This may be understood by looking at the diagram. The factor $cos θ 1$ has the effect of converting the effective emitting area $d A 1$ into a virtual projected area $cos θ 1 dA 1 = r 2 d Ω 2$ at right angles to the vector $r$ from source to detector. The solid angle $d Ω 1$ also has the effect of converting the detecting area $d A 2$ into a virtual projected area $cos θ 2 dA 2 = r 2 d Ω 1$ at right angles to the vector $r$ , so that $d Ω 1 = cos θ 2 dA 2 / r 2$ . Substituting this for $d Ω 1$ in the above expression for the collected energy $dE$ , one finds $dE = I (x, t; r 1, ν) cos θ 1 dA 1 cos θ 2 dA 2 dν dt / r 2$ : when the emitting and detecting areas and angles $dA 1$ and $dA 2$ , $θ 1$ and $θ 2$ , are held constant, the collected energy $dE$ is inversely proportional to the square of the distance $r$ between them, with invariant $I (x, t; r 1, ν)$ .

This may be expressed also by the statement that $I (x, t; r 1, ν)$ is invariant with respect to the length $r$ of $r$ ; that is to say, provided the optical devices have adequate resolution, and that the transmitting medium is perfectly transparent, as for example a vacuum, then the specific intensity of the source is unaffected by the length $r$ of the ray $r$ .^[12]^[14]^[15]

For the propagation of light in a transparent medium with a non-unit non-uniform refractive index, the invariant quantity along a ray is the specific intensity divided by the square of the absolute refractive index.^[16]

Reciprocity

For the propagation of light in a semi-transparent medium, specific intensity is not invariant along a ray, because of absorption and emission. Nevertheless, the Stokes-Helmholtz reversion-reciprocity principle applies, because absorption and emission are the same for both senses of a given direction at a point in a stationary medium.

Étendue and reciprocity

The term étendue is used to focus attention specifically on the geometrical aspects. The reciprocal character of étendue is indicated in the article about it. Étendue is defined as a second differential. In the notation of the present article, the second differential of the étendue, $d 2 G$ , of the pencil of light which "connects" the two surface elements $dA 1$ and $dA 2$ is defined as

d^{2}G=dA_{1}\cos(\theta _{1})\,d\Omega _{1}={\frac {dA_{1}\,dA_{2}\cos(\theta _{1})\cos(\theta _{2})}{r^{2}}}=dA_{2}\cos(\theta _{2})\,d\Omega _{2}.

This can help understand the geometrical aspects of the Stokes-Helmholtz reversion-reciprocity principle.

Collimated beam

For the present purposes, the light from a star can be treated as a practically collimated beam, but apart from this, a collimated beam is rarely if ever found in nature, though artificially produced beams can be very nearly collimated. For some purposes the rays of the sun can be considered as practically collimated, because the sun subtends an angle of only 32′ of arc.^[17] The specific (radiative) intensity is suitable for the description of an uncollimated radiative field. The integrals of specific (radiative) intensity with respect to solid angle, used for the definition of spectral flux density, are singular for exactly collimated beams, or may be viewed as Dirac delta functions. Therefore, the specific (radiative) intensity is unsuitable for the description of a collimated beam, while spectral flux density is suitable for that purpose.^[18]

Rays

Specific (radiative) intensity is built on the idea of a pencil of rays of light.^[19]^[20]^[21]

In an optically isotropic medium, the rays are normals to the wavefronts, but in an optically anisotropic crystalline medium, they are in general at angles to those normals. That is to say, in an optically anisotropic crystal, the energy does not in general propagate at right angles to the wavefronts.^[22]^[23]

Alternative approaches

The specific (radiative) intensity is a radiometric concept. Related to it is the intensity in terms of the photon distribution function,^[5]^[24] which uses the metaphor^[25] of a particle of light that traces the path of a ray.

The idea common to the photon and the radiometric concepts is that the energy travels along rays.

Another way to describe the radiative field is in terms of the Maxwell electromagnetic field, which includes the concept of the wavefront. The rays of the radiometric and photon concepts are along the time-averaged Poynting vector of the Maxwell field.^[26] In an anisotropic medium, the rays are not in general perpendicular to the wavefront.^[22]^[23]

Related Research Articles

<span class="mw-page-title-main">Luminance</span> Photometric measure

Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls within a given solid angle.

In optics, Lambert's cosine law says that the radiant intensity or luminous intensity observed from an ideal diffusely reflecting surface or ideal diffuse radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal; I = I₀ cos θ. The law is also known as the cosine emission law or Lambert's emission law. It is named after Johann Heinrich Lambert, from his Photometria, published in 1760.

<span class="mw-page-title-main">Reflectance</span> Capacity of an object to reflect light

The reflectance of the surface of a material is its effectiveness in reflecting radiant energy. It is the fraction of incident electromagnetic power that is reflected at the boundary. Reflectance is a component of the response of the electronic structure of the material to the electromagnetic field of light, and is in general a function of the frequency, or wavelength, of the light, its polarization, and the angle of incidence. The dependence of reflectance on the wavelength is called a reflectance spectrum or spectral reflectance curve.

In physics, the intensity or flux of radiant energy is the power transferred per unit area, where the area is measured on the plane perpendicular to the direction of propagation of the energy. In the SI system, it has units watts per square metre (W/m²), or kg⋅s⁻³ in base units. Intensity is used most frequently with waves such as acoustic waves (sound) or electromagnetic waves such as light or radio waves, in which case the average power transfer over one period of the wave is used. Intensity can be applied to other circumstances where energy is transferred. For example, one could calculate the intensity of the kinetic energy carried by drops of water from a garden sprinkler.

Brightness temperature or radiance temperature is a measure of the intensity of electromagnetic energy coming from a source. In particular, it is the temperature at which a black body would have to be in order to duplicate the observed intensity of a grey body object at a frequency $. This concept is used in radio astronomy, planetary science, materials science and climatology.$

Fourier-transform spectroscopy is a measurement technique whereby spectra are collected based on measurements of the coherence of a radiative source, using time-domain or space-domain measurements of the radiation, electromagnetic or not. It can be applied to a variety of types of spectroscopy including optical spectroscopy, infrared spectroscopy, nuclear magnetic resonance (NMR) and magnetic resonance spectroscopic imaging (MRSI), mass spectrometry and electron spin resonance spectroscopy.

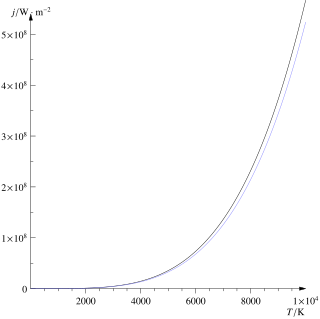
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.

Thermal radiation is electromagnetic radiation emitted by the thermal motion of particles in matter. Thermal radiation transmits as an electromagnetic wave through both matter and vacuum. When matter absorbs thermal radiation its temperature will tend to rise. All matter with a temperature greater than absolute zero emits thermal radiation. The emission of energy arises from a combination of electronic, molecular, and lattice oscillations in a material. Kinetic energy is converted to electromagnetism due to charge-acceleration or dipole oscillation. At room temperature, most of the emission is in the infrared (IR) spectrum. Thermal radiation is one of the fundamental mechanisms of heat transfer, along with conduction and convection.

In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature $T$ , when there is no net flow of matter or energy between the body and its environment.

The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was the prediction of late 19th century to early 20th century classical physics that an ideal black body at thermal equilibrium would emit an unbounded quantity of energy as wavelength decreased into the ultraviolet range. The term "ultraviolet catastrophe" was first used in 1911 by Paul Ehrenfest, but the concept originated with the 1900 statistical derivation of the Rayleigh–Jeans law.

In radiometry, radiance is the radiant flux emitted, reflected, transmitted or received by a given surface, per unit solid angle per unit projected area. Radiance is used to characterize diffuse emission and reflection of electromagnetic radiation, and to quantify emission of neutrinos and other particles. The SI unit of radiance is the watt per steradian per square metre. It is a directional quantity: the radiance of a surface depends on the direction from which it is being observed.

In radiometry, irradiance is the radiant flux received by a surface per unit area. The SI unit of irradiance is the watt per square metre (W⋅m⁻²). The CGS unit erg per square centimetre per second (erg⋅cm⁻²⋅s⁻¹) is often used in astronomy. Irradiance is often called intensity, but this term is avoided in radiometry where such usage leads to confusion with radiant intensity. In astrophysics, irradiance is called radiant flux.

In heat transfer, Kirchhoff's law of thermal radiation refers to wavelength-specific radiative emission and absorption by a material body in thermodynamic equilibrium, including radiative exchange equilibrium. It is a special case of Onsager reciprocal relations as a consequence of the time reversibility of microscopic dynamics, also known as microscopic reversibility.

Black-body radiation is the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body. It has a specific, continuous spectrum of wavelengths, inversely related to intensity, that depend only on the body's temperature, which is assumed, for the sake of calculations and theory, to be uniform and constant.

In radiometry, radiant intensity is the radiant flux emitted, reflected, transmitted or received, per unit solid angle, and spectral intensity is the radiant intensity per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. These are directional quantities. The SI unit of radiant intensity is the watt per steradian, while that of spectral intensity in frequency is the watt per steradian per hertz and that of spectral intensity in wavelength is the watt per steradian per metre —commonly the watt per steradian per nanometre. Radiant intensity is distinct from irradiance and radiant exitance, which are often called intensity in branches of physics other than radiometry. In radio-frequency engineering, radiant intensity is sometimes called radiation intensity.

In atomic, molecular, and optical physics, the Einstein coefficients are quantities describing the probability of absorption or emission of a photon by an atom or molecule. The Einstein A coefficients are related to the rate of spontaneous emission of light, and the Einstein B coefficients are related to the absorption and stimulated emission of light. Throughout this article, "light" refers to any electromagnetic radiation, not necessarily in the visible spectrum.

<span class="mw-page-title-main">Isotropic radiator</span>

An isotropic radiator is a theoretical point source of waves which radiates the same intensity of radiation in all directions. It may be based on sound waves or electromagnetic waves, in which case it is also known as an isotropic antenna. It has no preferred direction of radiation, i.e., it radiates uniformly in all directions over a sphere centred on the source.

Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.

The linear attenuation coefficient, attenuation coefficient, or narrow-beam attenuation coefficient characterizes how easily a volume of material can be penetrated by a beam of light, sound, particles, or other energy or matter. A coefficient value that is large represents a beam becoming 'attenuated' as it passes through a given medium, while a small value represents that the medium had little effect on loss. The (derived) SI unit of attenuation coefficient is the reciprocal metre (m⁻¹). Extinction coefficient is another term for this quantity, often used in meteorology and climatology. Most commonly, the quantity measures the exponential decay of intensity, that is, the value of downward e-folding distance of the original intensity as the energy of the intensity passes through a unit thickness of material, so that an attenuation coefficient of 1 m⁻¹ means that after passing through 1 metre, the radiation will be reduced by a factor of e, and for material with a coefficient of 2 m⁻¹, it will be reduced twice by e, or e². Other measures may use a different factor than e, such as the decadic attenuation coefficient below. The broad-beam attenuation coefficient counts forward-scattered radiation as transmitted rather than attenuated, and is more applicable to radiation shielding. The mass attenuation coefficient is the attenuation coefficient normalized by the density of the material.

In spectroscopy, spectral flux density is the quantity that describes the rate at which energy is transferred by electromagnetic radiation through a real or virtual surface, per unit surface area and per unit wavelength. It is a radiometric rather than a photometric measure. In SI units it is measured in W m⁻³, although it can be more practical to use W m⁻² nm⁻¹ or W m⁻² μm⁻¹, and respectively by W·m⁻²·Hz⁻¹, Jansky or solar flux units. The terms irradiance, radiant exitance, radiant emittance, and radiosity are closely related to spectral flux density.

References

↑ Palmer, James M. "The SI system and SI units for Radiometry and photometry" (PDF). Archived from the original (PDF) on August 2, 2012.
↑ Rowlett, Russ. "How Many? A Dictionary of Units of Measurement" . Retrieved 10 August 2012.
1 2 3 Planck, M. (1914) The Theory of Heat Radiation, second edition translated by M. Masius, P. Blakiston's Son and Co., Philadelphia, pages 13-15.
1 2 Chandrasekhar, S. (1950). Radiative Transfer, Oxford University Press, Oxford, pages 1-2.
1 2 3 Mihalas, D., Weibel-Mihalas, B. (1984). Foundations of Radiation Hydrodynamics, Oxford University Press, New York ISBN 0-19-503437-6., pages 311-312.
↑ Goody, R.M., Yung, Y.L. (1989). Atmospheric Radiation: Theoretical Basis, 2nd edition, Oxford University Press, Oxford, New York, 1989, ISBN 0-19-505134-3, page 16.
↑ Liou, K.N. (2002). An Introduction of Atmospheric Radiation, second edition, Academic Press, Amsterdam, ISBN 978-0-12-451451-5, page 4.
↑ Hapke, B. (1993). Theory of Reflectance and Emittance Spectroscopy, Cambridge University Press, Cambridge UK, ISBN 0-521-30789-9, page 64.
↑ Rybicki, G.B., Lightman, A.P. (1979/2004). Radiative Processes in Astrophysics, reprint, John Wiley & Sons, New York, ISBN 0-471-04815-1, page 3.
↑ Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light , 7th edition, Cambridge University Press, ISBN 0-521-64222-1, page 194.
↑ Kondratyev, K.Y. (1969). Radiation in the Atmosphere, Academic Press, New York, page 10.
1 2 3 Mihalas, D. (1978). Stellar Atmospheres, 2nd edition, Freeman, San Francisco, ISBN 0-7167-0359-9, pages 2-5.
↑ Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light, 7th edition, Cambridge University Press, ISBN 0-521-64222-1, pages 194-199.
1 2 Rybicki, G.B., Lightman, A.P. (1979). Radiative Processes in Astrophysics, John Wiley & Sons, New York, ISBN 0-471-04815-1, pages 7-8.
↑ Bohren, C.F., Clothiaux, E.E. (2006). Fundamentals of Atmospheric Radiation, Wiley-VCH, Weinheim, ISBN 3-527-40503-8, pages 191-192.
↑ Planck, M. (1914). The Theory of Heat Radiation, second edition translated by M. Masius, P. Blakiston's Son and Co., Philadelphia, page 35.
↑ Goody, R.M., Yung, Y.L. (1989). Atmospheric Radiation: Theoretical Basis, 2nd edition, Oxford University Press, Oxford, New York, 1989, ISBN 0-19-505134-3, page 18.
↑ Hapke, B. (1993). Theory of Reflectance and Emittance Spectroscopy, Cambridge University Press, Cambridge UK, ISBN 0-521-30789-9, see pages 12 and 64.
↑ Planck, M. (1914). The Theory of Heat Radiation, second edition translated by M. Masius, P. Blakiston's Son and Co., Philadelphia, Chapter 1.
↑ Levi, L. (1968). Applied Optics: A Guide to Optical System Design, 2 volumes, Wiley, New York, volume 1, pages 119-121.
↑ Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light, 7th edition, Cambridge University Press, ISBN 0-521-64222-1, pages 116-125.
1 2 Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light, 7th edition, Cambridge University Press, ISBN 0-521-64222-1, pages 792-795.
1 2 Hecht, E., Zajac, A. (1974). Optics, Addison-Wesley, Reading MA, page 235.
↑ Mihalas, D. (1978). Stellar Atmospheres, 2nd edition, Freeman, San Francisco, ISBN 0-7167-0359-9, page 10.
↑ Lamb, W.E., Jr (1995). Anti-photon, Applied Physics, B60: 77-84.
↑ Mihalas, D. (1978). Stellar Atmospheres, 2nd edition, Freeman, San Francisco, ISBN 0-7167-0359-9, page 11.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Palmer, James M. "The SI system and SI units for Radiometry and photometry" (PDF). Archived from the original (PDF) on August 2, 2012.

[2] Rowlett, Russ. "How Many? A Dictionary of Units of Measurement" . Retrieved 10 August 2012.

[Planck_1914-3] 1 2 3 Planck, M. (1914) The Theory of Heat Radiation, second edition translated by M. Masius, P. Blakiston's Son and Co., Philadelphia, pages 13-15.

[Chandrasekhar_1950-4] 1 2 Chandrasekhar, S. (1950). Radiative Transfer, Oxford University Press, Oxford, pages 1-2.

[Mihalas_Mihalas_1984-5] 1 2 3 Mihalas, D., Weibel-Mihalas, B. (1984). Foundations of Radiation Hydrodynamics, Oxford University Press, New York ISBN 0-19-503437-6., pages 311-312.

[6] Goody, R.M., Yung, Y.L. (1989). Atmospheric Radiation: Theoretical Basis, 2nd edition, Oxford University Press, Oxford, New York, 1989, ISBN 0-19-505134-3, page 16.

[7] Liou, K.N. (2002). An Introduction of Atmospheric Radiation, second edition, Academic Press, Amsterdam, ISBN 978-0-12-451451-5, page 4.

[Hapke_64-8] Hapke, B. (1993). Theory of Reflectance and Emittance Spectroscopy, Cambridge University Press, Cambridge UK, ISBN 0-521-30789-9, page 64.

[9] Rybicki, G.B., Lightman, A.P. (1979/2004). Radiative Processes in Astrophysics, reprint, John Wiley & Sons, New York, ISBN 0-471-04815-1, page 3.

[10] Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light , 7th edition, Cambridge University Press, ISBN 0-521-64222-1, page 194.

[Kondratyev_1969-11] Kondratyev, K.Y. (1969). Radiation in the Atmosphere, Academic Press, New York, page 10.

[Mihalas_1978-12] 1 2 3 Mihalas, D. (1978). Stellar Atmospheres, 2nd edition, Freeman, San Francisco, ISBN 0-7167-0359-9, pages 2-5.

[13] Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light, 7th edition, Cambridge University Press, ISBN 0-521-64222-1, pages 194-199.

[RL_1979-14] 1 2 Rybicki, G.B., Lightman, A.P. (1979). Radiative Processes in Astrophysics, John Wiley & Sons, New York, ISBN 0-471-04815-1, pages 7-8.

[15] Bohren, C.F., Clothiaux, E.E. (2006). Fundamentals of Atmospheric Radiation, Wiley-VCH, Weinheim, ISBN 3-527-40503-8, pages 191-192.

[Planck_1914_p_35-16] Planck, M. (1914). The Theory of Heat Radiation, second edition translated by M. Masius, P. Blakiston's Son and Co., Philadelphia, page 35.

[17] Goody, R.M., Yung, Y.L. (1989). Atmospheric Radiation: Theoretical Basis, 2nd edition, Oxford University Press, Oxford, New York, 1989, ISBN 0-19-505134-3, page 18.

[18] Hapke, B. (1993). Theory of Reflectance and Emittance Spectroscopy, Cambridge University Press, Cambridge UK, ISBN 0-521-30789-9, see pages 12 and 64.

[19] Planck, M. (1914). The Theory of Heat Radiation, second edition translated by M. Masius, P. Blakiston's Son and Co., Philadelphia, Chapter 1.

[20] Levi, L. (1968). Applied Optics: A Guide to Optical System Design, 2 volumes, Wiley, New York, volume 1, pages 119-121.

[21] Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light, 7th edition, Cambridge University Press, ISBN 0-521-64222-1, pages 116-125.

[BW_1999_792-795-22] 1 2 Born, M., Wolf, E. (1999). Principles of Optics: Electromagnetic theory of propagation, interference and diffraction of light, 7th edition, Cambridge University Press, ISBN 0-521-64222-1, pages 792-795.

[HJ-23] 1 2 Hecht, E., Zajac, A. (1974). Optics, Addison-Wesley, Reading MA, page 235.

[Mihalas_1978_10-24] Mihalas, D. (1978). Stellar Atmospheres, 2nd edition, Freeman, San Francisco, ISBN 0-7167-0359-9, page 10.

[25] Lamb, W.E., Jr (1995). Anti-photon, Applied Physics, B60: 77-84.

[26] Mihalas, D. (1978). Stellar Atmospheres, 2nd edition, Freeman, San Francisco, ISBN 0-7167-0359-9, page 11.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]