Stability (probability)

Last updated

In probability theory, the stability of a random variable is the property that a linear combination of two independent copies of the variable has the same distribution, up to location and scale parameters. [1] The distributions of random variables having this property are said to be "stable distributions". Results available in probability theory show that all possible distributions having this property are members of a four-parameter family of distributions. The article on the stable distribution describes this family together with some of the properties of these distributions.

Contents

The importance in probability theory of "stability" and of the stable family of probability distributions is that they are "attractors" for properly normed sums of independent and identically distributed random variables.

Important special cases of stable distributions are the normal distribution, the Cauchy distribution and the Lévy distribution. For details see stable distribution.

Definition

There are several basic definitions for what is meant by stability. Some are based on summations of random variables and others on properties of characteristic functions.

Definition via distribution functions

Feller [2] makes the following basic definition. A random variable X is called stable (has a stable distribution) if, for n independent copies Xi of X, there exist constants cn > 0 and dn such that

where this equality refers to equality of distributions. A conclusion drawn from this starting point is that the sequence of constants cn must be of the form

 for 

A further conclusion is that it is enough for the above distributional identity to hold for n=2 and n=3 only. [3]

Stability in probability theory

There are a number of mathematical results that can be derived for distributions which have the stability property. That is, all possible families of distributions which have the property of being closed under convolution are being considered. [4] It is convenient here to call these stable distributions, without meaning specifically the distribution described in the article named stable distribution, or to say that a distribution is stable if it is assumed that it has the stability property. The following results can be obtained for univariate distributions which are stable.

Other types of stability

The above concept of stability is based on the idea of a class of distributions being closed under a given set of operations on random variables, where the operation is "summation" or "averaging". Other operations that have been considered include:

See also

Notes

  1. ↑ Lukacs, E. (1970) Section 5.7
  2. ↑ Feller (1971), Section VI.1
  3. ↑ Feller (1971), Problem VI.13.3
  4. ↑ Lukacs, E. (1970) Section 5.7
  5. ↑ Lukacs, E. (1970) Theorem 5.7.1
  6. ↑ Lukacs, E. (1970) Theorem 5.8.1
  7. ↑ Lukacs, E. (1970) Theorem 5.10.1
  8. ↑ Klebanov et al. (1984)

Related Research Articles

There are several kinds of mean in mathematics, especially in statistics.

Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of these outcomes is called an event.

In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.

Geometric distribution probability distribution

In probability theory and statistics, the geometric distribution is either of two discrete probability distributions:

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesXi are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable Xi in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.

Zeta distribution probability distribution on the integers in which the probability of a number is inversely proportion to a fixed power of the number

In probability theory and statistics, the zeta distribution is a discrete probability distribution. If X is a zeta-distributed random variable with parameter s, then the probability that X takes the integer value k is given by the probability mass function

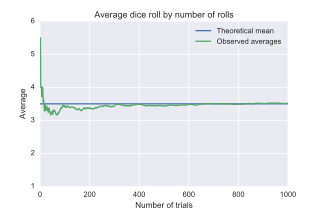
Law of large numbers Theorem in probability and statistics

In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and will tend to become closer to the expected value as more trials are performed.

In probability theory, de Finetti's theorem states that exchangeable observations are conditionally independent relative to some latent variable. An epistemic probability distribution could then be assigned to this variable. It is named in honor of Bruno de Finetti.

In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. In the simplest cases, the result can be either a continuous or a discrete distribution.

In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk.

Stable distribution distribution of variables which satisfies a stability property under linear combinations

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.

Characteristic function (probability theory) real-valued random variable completely defines its probability distribution

In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables.

In probability theory, an indecomposable distribution is a probability distribution that cannot be represented as the distribution of the sum of two or more non-constant independent random variables: Z ≠ X + Y. If it can be so expressed, it is decomposable:Z = X + Y. If, further, it can be expressed as the distribution of the sum of two or more independent identically distributed random variables, then it is divisible:Z = X1 + X2.

In probability theory, a probability distribution is infinitely divisible if it can be expressed as the probability distribution of the sum of an arbitrary number of independent and identically distributed random variables. The characteristic function of any infinitely divisible distribution is then called an infinitely divisible characteristic function.

Financial models with long-tailed distributions and volatility clustering have been introduced to overcome problems with the realism of classical financial models. These classical models of financial time series typically assume homoskedasticity and normality cannot explain stylized phenomena such as skewness, heavy tails, and volatility clustering of the empirical asset returns in finance. In 1963, Benoit Mandelbrot first used the stable distribution to model the empirical distributions which have the skewness and heavy-tail property. Since -stable distributions have infinite -th moments for all , the tempered stable processes have been proposed for overcoming this limitation of the stable distribution.

In game theory a Poisson game is a game with a random number of players, where the distribution of the number of players follows a Poisson random process. An extension of games of imperfect information, Poisson games have mostly seen application to models of voting.

A geometric stable distribution or geo-stable distribution is a type of leptokurtic probability distribution. Geometric stable distributions were introduced in Klebanov, L. B., Maniya, G. M., and Melamed, I. A. (1985). A problem of Zolotarev and analogs of infinitely divisible and stable distributions in a scheme for summing a random number of random variables. These distributions are analogues for stable distributions for the case when the number of summands is random, independent of the distribution of summand, and having geometric distribution. The geometric stable distribution may be symmetric or asymmetric. A symmetric geometric stable distribution is also referred to as a Linnik distribution. The Laplace distribution and asymmetric Laplace distribution are special cases of the geometric stable distribution. The Laplace distribution is also a special case of a Linnik distribution. The Mittag-Leffler distribution is also a special case of a geometric stable distribution.

The discrete-stable distributions are a class of probability distributions with the property that the sum of several random variables from such a distribution is distributed according to the same family. They are the discrete analogue of the continuous-stable distributions.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.