 | Unsolved problem in mathematics: Is every group surjunctive? (more unsolved problems in mathematics) |
In mathematics, a surjunctive group is a group such that every injective cellular automaton with the group elements as its cells is also surjective. Surjunctive groups were introduced by Gottschalk (1973). It is unknown whether every group is surjunctive.
A cellular automaton consists of a regular system of cells, each containing a symbol from a finite alphabet, together with a uniform rule called a transition function for updating all cells simultaneously based on the values of neighboring cells. Most commonly the cells are arranged in the form of a line or a higher-dimensional integer grid, but other arrangements of cells are also possible. What is required of the cells is that they form a structure in which every cell "looks the same as" every other cell: there is a symmetry of both the arrangement of cells and the rule set that takes any cell to any other cell. Mathematically, this can be formalized by the notion of a group, a set of elements together with an associative and invertible binary operation. The elements of the group can be used as the cells of an automaton, with symmetries generated by the group operation. For instance, a one-dimensional line of cells can be described in this way as the additive group of the integers, and the higher-dimensional integer grids can be described as the free abelian groups.
The collection of all possible states of a cellular automaton over a group can be described as the functions that map each group element to one of the symbols in the alphabet. As a finite set, the alphabet has a discrete topology, and the collection of states can be given the product topology (called a prodiscrete topology because it is the product of discrete topologies). To be the transition function of a cellular automaton, a function from states to states must be a continuous function for this topology, and must also be equivariant with the group action, meaning that shifting the cells prior to applying the transition function produces the same result as applying the function and then shifting the cells. For such functions, the Curtis–Hedlund–Lyndon theorem ensures that the value of the transition function at each group element depends on the previous state of only a finite set of neighboring elements.
A state transition function is a surjective function when every state has a predecessor (there can be no Garden of Eden). It is an injective function when no two states have the same successor. A surjunctive group is a group with the property that, when its elements are used as the cells of cellular automata, every injective transition function of a cellular automaton is also surjective. Equivalently, summarizing the definitions above, a group is surjunctive if, for every finite set , every continuous equivariant injective function is also surjective. [1] The implication from injectivity to surjectivity is a form of the Garden of Eden theorem, and the cellular automata defined from injective and surjective transition functions are reversible.
Examples of surjunctive groups include all locally residually finite groups, [2] all free groups, [2] all subgroups of surjunctive groups, [3] all abelian groups, [2] all sofic groups, [4] and every locally surjunctive group. [3]
When he introduced surjunctive groups in 1973, Gottschalk observed that there were no known examples of non-surjunctive groups. As of 2014, it is still unknown whether every group is surjunctive. [5]
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A countable set is either a finite set or a countably infinite set. Whether finite or infinite, the elements of a countable set can always be counted one at a time and, although the counting may never finish, every element of the set is associated with a unique natural number.
In mathematics, an endomorphism is a morphism from a mathematical object to itself. An endomorphism that is also an isomorphism is an automorphism. For example, an endomorphism of a vector space V is a linear map f: V → V, and an endomorphism of a group G is a group homomorphism f: G → G. In general, we can talk about endomorphisms in any category. In the category of sets, endomorphisms are functions from a set S to itself.
In mathematics, a group is a set equipped with a binary operation that combines any two elements to form a third element in such a way that four conditions called group axioms are satisfied, namely closure, associativity, identity and invertibility. One of the most familiar examples of a group is the set of integers together with the addition operation, but groups are encountered in numerous areas within and outside mathematics, and help focusing on essential structural aspects, by detaching them from the concrete nature of the subject of the study.
In mathematics, a partial function from X to Y is a function f: X′ → Y, for some subset X′ of X. It generalizes the concept of a function f : X → Y by not forcing f to map every element of X to an element of Y. If X′ = X, then f is called a total function for emphasizing that its domain is not a proper subset of X. Partial functions are often used when the exact domain, X, is not known. In real and complex analysis, a partial function is generally called simply a function.
In mathematics, profinite groups are topological groups that are in a certain sense assembled from finite groups. They share many properties with their finite quotients: for example, both Lagrange's theorem and the Sylow theorems generalise well to profinite groups.
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using a regular expression, in the strict sense of the latter notion used in theoretical computer science.
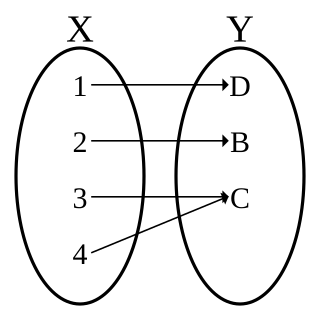
In mathematics, a function f from a set X to a set Y is surjective, if for every element y in the codomain Y of f, there is at least one element x in the domain X of f such that f(x) = y. It is not required that x be unique; the function f may map one or more elements of X to the same element of Y.
A cellular automaton is a discrete model studied in computer science, mathematics, physics, complexity science, theoretical biology and microstructure modeling. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays.
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science and discrete mathematics. The word automata comes from the Greek word αὐτόματα, which means "self-making".
In mathematics, a free abelian group or free Z-module is an abelian group with a basis, or, equivalently, a free module over the integers. Being an abelian group means that it is a set with an addition operation that is associative, commutative, and invertible. A basis is a subset such that every element of the group can be uniquely expressed as a linear combination of basis elements with integer coefficients. For instance, the integers with addition form a free abelian group with basis {1}.
In mathematics and computer science, the Krohn–Rhodes theory is an approach to the study of finite semigroups and automata that seeks to decompose them in terms of elementary components. These components correspond to finite aperiodic semigroups and finite simple groups that are combined together in a feedback-free manner.
In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.
In mathematics and theoretical computer science, an automatic sequence is an infinite sequence of terms characterized by a finite automaton. The n-th term of an automatic sequence a(n) is a mapping of the final state reached in a finite automaton accepting the digits of the number n in some fixed base k.
In the mathematical study of cellular automata, Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value. In each time step all values are simultaneously replaced by the exclusive or of their two neighboring values. Martin, Odlyzko & Wolfram (1984) call it "the simplest non-trivial cellular automaton", and it is described extensively in Stephen Wolfram's 2002 book A New Kind of Science.
The Curtis–Hedlund–Lyndon theorem is a mathematical characterization of cellular automata in terms of their symbolic dynamics. It is named after Morton L. Curtis, Gustav A. Hedlund, and Roger Lyndon; in his 1969 paper stating the theorem, Hedlund credited Curtis and Lyndon as co-discoverers. It has been called "one of the fundamental results in symbolic dynamics".
In mathematics, the Ax–Grothendieck theorem is a result about injectivity and surjectivity of polynomials that was proved independently by James Ax and Alexander Grothendieck.
A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
In mathematics, a sofic group is a group whose Cayley graph is an initially subamenable graph, or equivalently a subgroup of an ultraproduct of finite-rank symmetric groups such that every two elements of the group have distance 1. They were introduced by Gromov (1999) as a common generalization of amenable and residually finite groups. The name "sofic", from the Hebrew word סופי meaning "finite", was later applied by Weiss (2000), following Weiss's earlier use of the same word to indicate a generalization of finiteness in sofic subshifts.
Critters is a reversible block cellular automaton with similar dynamics to Conway's Game of Life, first described by Tommaso Toffoli and Norman Margolus in 1987.
In mathematics, the Muller–Schupp theorem states that a finitely generated group G has context-free word problem if and only if G is virtually free. The theorem was proved by David Muller and Paul Schupp in 1983.
