
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as
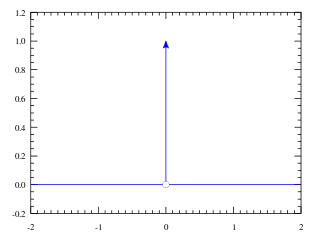
In mathematical physics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.

Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system with conservative forces has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries over physical space.

The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.

In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).

Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.

The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.

The Schwinger–Dyson equations (SDEs) or Dyson–Schwinger equations, named after Julian Schwinger and Freeman Dyson, are general relations between correlation functions in quantum field theories (QFTs). They are also referred to as the Euler–Lagrange equations of quantum field theories, since they are the equations of motion corresponding to the Green's function. They form a set of infinitely many functional differential equations, all coupled to each other, sometimes referred to as the infinite tower of SDEs.

Level-set methods (LSM) are a conceptual framework for using level sets as a tool for numerical analysis of surfaces and shapes. The advantage of the level-set model is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects. Also, the level-set method makes it very easy to follow shapes that change topology, for example, when a shape splits in two, develops holes, or the reverse of these operations. All these make the level-set method a great tool for modeling time-varying objects, like inflation of an airbag, or a drop of oil floating in water.

In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form
In mathematics, in the area of wavelet analysis, a refinable function is a function which fulfils some kind of self-similarity. A function is called refinable with respect to the mask if
In numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high-resolution schemes for the numerical solution of partial differential equations.
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating derivatives with finite differences. Both the spatial domain and time interval are discretized, or broken into a finite number of steps, and the value of the solution at these discrete points is approximated by solving algebraic equations containing finite differences and values from nearby points.
In applied mathematics, discontinuous Galerkin methods (DG methods) form a class of numerical methods for solving differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic, parabolic and mixed form problems arising from a wide range of applications. DG methods have in particular received considerable interest for problems with a dominant first-order part, e.g. in electrodynamics, fluid mechanics and plasma physics.
In fluid dynamics, The projection method is an effective means of numerically solving time-dependent incompressible fluid-flow problems. It was originally introduced by Alexandre Chorin in 1967 as an efficient means of solving the incompressible Navier-Stokes equations. The key advantage of the projection method is that the computations of the velocity and the pressure fields are decoupled.
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.
Unsteady flows are characterized as flows in which the properties of the fluid are time dependent. It gets reflected in the governing equations as the time derivative of the properties are absent. For Studying Finite-volume method for unsteady flow there is some governing equations >
The convection–diffusion equation describes the flow of heat, particles, or other physical quantities in situations where there is both diffusion and convection or advection. For information about the equation, its derivation, and its conceptual importance and consequences, see the main article convection–diffusion equation. This article describes how to use a computer to calculate an approximate numerical solution of the discretized equation, in a time-dependent situation.


































