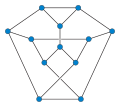
Edge coloring and perfect matchings
Edge coloring Tietze's graph requires four colors; that is, its chromatic index is 4. Equivalently, the edges of Tietze's graph can be partitioned into four matchings, but no fewer.
Tietze's graph matches part of the definition of a snark: it is a cubic bridgeless graph that is not 3-edge-colorable. However, most authors restrict snarks to graphs without 3-cycles, so Tietze's graph is not generally considered to be a snark. Nevertheless, it is isomorphic to the graph J3, part of an infinite family of flower snarks introduced by R. Isaacs in 1975. [5]
Unlike the Petersen graph, the Tietze graph can be covered by four perfect matchings. This property plays a key role in a proof that testing whether a graph can be covered by four perfect matchings is NP-complete. [6]

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.
In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into k independent sets and there is no way to partition them into k − 1 independent sets.

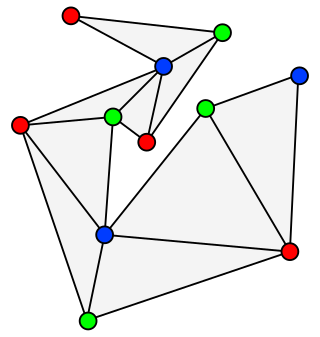
In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.
In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.

In graph-theoretic mathematics, a cycle double cover is a collection of cycles in an undirected graph that together include each edge of the graph exactly twice. For instance, for any polyhedral graph, the faces of a convex polyhedron that represents the graph provide a double cover of the graph: each edge belongs to exactly two faces.

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.
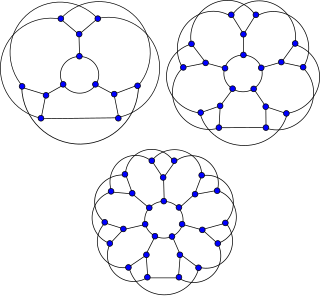
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.

In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the dimension-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason, who used it to evaluate the Ramsey number R(3,3,3) = 17.

In the mathematical field of graph theory, the Nauru graph is a symmetric, bipartite, cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.
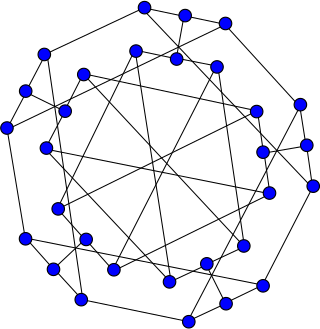
In the mathematical field of graph theory, the double-star snark is a snark with 30 vertices and 45 edges.
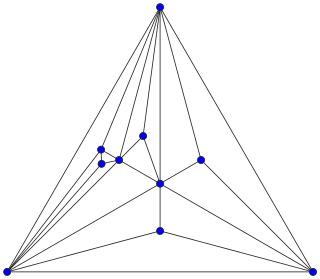
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

In the mathematical discipline of graph theory, Petersen's theorem, named after Julius Petersen, is one of the earliest results in graph theory and can be stated as follows:
Petersen's Theorem. Every cubic, bridgeless graph contains a perfect matching.

The Petersen Graph is a mathematics book about the Petersen graph and its applications in graph theory. It was written by Derek Holton and John Sheehan, and published in 1993 by the Cambridge University Press as volume 7 in their Australian Mathematical Society Lecture Series.