 | This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations .(June 2015) (Learn how and when to remove this template message) |
A torus bundle, in the sub-field of geometric topology in mathematics, is a kind of surface bundle over the circle, which in turn is a class of three-manifolds.
To obtain a torus bundle: let be an orientation-preserving homeomorphism of the two-dimensional torus to itself. Then the three-manifold is obtained by
Then is the torus bundle with monodromy .
For example, if is the identity map (i.e., the map which fixes every point of the torus) then the resulting torus bundle is the three-torus: the Cartesian product of three circles.
Seeing the possible kinds of torus bundles in more detail requires an understanding of William Thurston's geometrization program. Briefly, if is finite order, then the manifold has Euclidean geometry. If is a power of a Dehn twist then has Nil geometry. Finally, if is an Anosov map then the resulting three-manifold has Sol geometry.
These three cases exactly correspond to the three possibilities for the absolute value of the trace of the action of on the homology of the torus: either less than two, equal to two, or greater than two.
In mathematics, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.
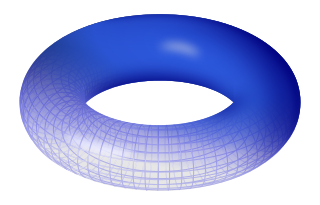
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.
In mathematics, homology is a general way of associating a sequence of algebraic objects such as abelian groups or modules to other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry.
In differential geometry, a (smooth) Riemannian manifold or (smooth) Riemannian space(M, g) is a real, smooth manifold M equipped with an inner product gp on the tangent space TpM at each point p that varies smoothly from point to point in the sense that if X and Y are differentiable vector fields on M, then p ↦ gp(X|p, Y|p) is a smooth function. The family gp of inner products is called a Riemannian metric. These terms are named after the German mathematician Bernhard Riemann. The study of Riemannian manifolds constitutes the subject called Riemannian geometry.
This is a glossary of terms specific to differential geometry and differential topology. The following three glossaries are closely related:
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.
In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, more precisely in topology and differential geometry, a hyperbolic 3–manifold is a manifold of dimension 3 equipped with a hyperbolic metric, that is a Riemannian metric which has all its sectional curvatures equal to -1. It is generally required that this metric be also complete: in this case the manifold can be realised as a quotient of the 3-dimensional hyperbolic space by a discrete group of isometries.
In mathematics, an atoroidal 3-manifold is one that does not contain an essential torus. There are two major variations in this terminology: an essential torus may be defined geometrically, as an embedded, non-boundary parallel, incompressible torus, or it may be defined algebraically, as a subgroup of its fundamental group that is not conjugate to a peripheral subgroup. The terminology is not standardized, and different authors require atoroidal 3-manifolds to satisfy certain additional restrictions. For instance:
In mathematics, a solid torus is the topological space formed by sweeping a disk around a circle. It is homeomorphic to the Cartesian product of the disk and the circle, endowed with the product topology. A standard way to visualize a solid torus is as a toroid, embedded in 3-space. However, it should be distinguished from a torus, which has the same visual appearance: the torus is the two-dimensional space on the boundary of a toroid, while the solid torus includes also the compact interior space enclosed by the torus.
A Seifert fiber space is a 3-manifold together with a decomposition as a disjoint union of circles. In other words, it is a -bundle over a 2-dimensional orbifold. Most 3-manifolds are Seifert fiber spaces, and they account for all compact oriented manifolds in 6 of the 8 Thurston geometries of the geometrization conjecture.
In mathematics, a surface bundle over the circle is a fiber bundle with base space a circle, and with fiber space a surface. Therefore the total space has dimension 2 + 1 = 3. In general, fiber bundles over the circle are a special case of mapping tori.
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, each point of an n-dimensional manifold has a neighborhood that is homeomorphic to the Euclidean space of dimension n. In this more precise terminology, a manifold is referred to as an n-manifold.
In topology, a branch of mathematics, a topological manifold is a topological space which locally resembles real n-dimensional space in a sense defined below. Topological manifolds form an important class of topological spaces with applications throughout mathematics. All manifolds are topological manifolds by definition, but many manifolds may be equipped with additional structure. Every manifold has an "underlying" topological manifold, gotten by simply "forgetting" any additional structure the manifold has.
In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since each chart lies within a linear space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
The three-dimensional torus, or triple torus, is defined as the Cartesian product of three circles,
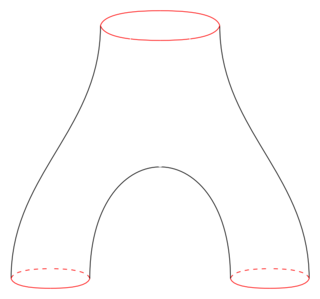
In mathematics, a pair of pants is a surface which is homeomorphic to the three-holed sphere. The name comes from considering one of the removed disks as the waist and the two others as the cuffs of a pair of pants.
In mathematics, a differentiable manifold of dimension n is called parallelizable if there exist smooth vector fields
In mathematics, the mapping torus in topology of a homeomorphism f of some topological space X to itself is a particular geometric construction with f. Take the cartesian product of X with a closed interval I, and glue the boundary components together by the static homeomorphism:
In differential geometry, the localization formula states: for an equivariantly closed equivariant differential form on an orbifold M with a torus action and for a sufficient small in the Lie algebra of the torus T,
