
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros.

Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra to study problems in geometry. The theory of plane and space curves and surfaces in the three-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century and the 19th century.

In mathematics, a plane real algebraic curve is the set of points on the Euclidean plane whose coordinates are zeros of some polynomial in two variables. More generally an algebraic curve is similar but may be embedded in a higher dimensional space or defined over some more general field.

Oscar Zariski was a Russian-born American mathematician and one of the most influential algebraic geometers of the 20th century.

Sir William Vallance Douglas Hodge was a British mathematician, specifically a geometer.
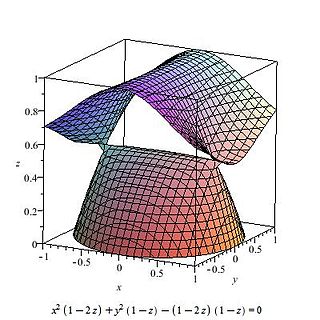
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single quaternary cubic polynomial which is homogeneous of degree 3. Cubic surfaces are del Pezzo surfaces.

Kunihiko Kodaira was a Japanese mathematician known for distinguished work in algebraic geometry and the theory of complex manifolds, and as the founder of the Japanese school of algebraic geometers. He was awarded a Fields Medal in 1954, being the first Japanese national to receive this honour.

In algebraic geometry, a Kummer quartic surface, first studied by Kummer (1864), is an irreducible nodal surface of degree 4 in with the maximal possible number of 16 double points. Any such surface is the Kummer variety of the Jacobian variety of a smooth hyperelliptic curve of genus 2; i.e. a quotient of the Jacobian by the Kummer involution x ↦ −x. The Kummer involution has 16 fixed points: the 16 2-torsion point of the Jacobian, and they are the 16 singular points of the quartic surface. Resolving the 16 double points of the quotient of a torus by the Kummer involution gives a K3 surface with 16 disjoint rational curves; these K3 surfaces are also sometimes called Kummer surfaces.

In the mathematical field of algebraic geometry, a singular point of an algebraic varietyV is a point P that is 'special', in the geometric sense that at this point the tangent space at the variety may not be regularly defined. In case of varieties defined over the reals, this notion generalizes the notion of local non-flatness. A point of an algebraic variety which is not singular is said to be regular. An algebraic variety which has no singular point is said to be non-singular or smooth.
In algebraic geometry, a tetrahedroid is a special kind of Kummer surface studied by Cayley (1846), with the property that the intersections with the faces of a fixed tetrahedron are given by two conics intersecting in four nodes. Tetrahedroids generalize Fresnel's wave surface.

In algebraic geometry, the Cayley surface, named after Arthur Cayley, is a cubic nodal surface in 3-dimensional projective space with four conical points. It can be given by the equation

In mathematics, an immersion is a differentiable function between differentiable manifolds whose derivative is everywhere injective. Explicitly, f : M → N is an immersion if
In algebraic geometry, a Weddle surface, introduced by Thomas Weddle, is a quartic surface in 3-dimensional projective space, given by the locus of vertices of the family of cones passing through 6 points in general position.
In algebraic geometry, a Plücker surface, studied by Julius Plücker (1899), is a quartic surface in 3-dimensional projective space with a double line and 8 nodes.
The terminology of algebraic geometry changed drastically during the twentieth century, with the introduction of the general methods, initiated by David Hilbert and the Italian school of algebraic geometry in the beginning of the century, and later formalized by André Weil, Jean-Pierre Serre and Alexander Grothendieck. Much of the classical terminology, mainly based on case study, was simply abandoned, with the result that books and papers written before this time can be hard to read. This article lists some of this classical terminology, and describes some of the changes in conventions.
This page is a glossary of terms in invariant theory. For descriptions of particular invariant rings, see invariants of a binary form, symmetric polynomials. For geometric terms used in invariant theory see the glossary of classical algebraic geometry. Definitions of many terms used in invariant theory can be found in, ,, ,, ,, , and the index to the fourth volume of Sylvester's collected works includes many of the terms invented by him.

Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics.

In computing, a Digital Object Identifier or DOI is a persistent identifier or handle used to uniquely identify objects, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.
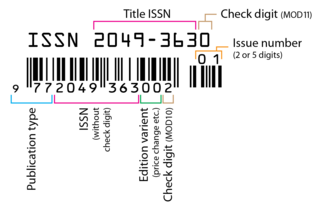
An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication, such as a magazine. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.















