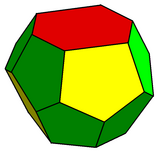
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, the truncated icosahedron is a polyhedron that can be constructed by truncating all of the regular icosahedron's vertices. Intuitively, it may be regarded as footballs that are typically patterned with white hexagons and black pentagons. It can be found in the application of geodesic dome structures such as those whose architecture Buckminster Fuller pioneered are often based on this structure. It is an example of an Archimedean solid, as well as a Goldberg polyhedron.

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron.
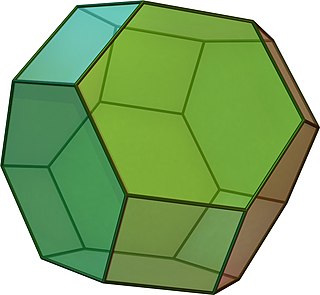
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In geometry, an n-gonaltrapezohedron, n-trapezohedron, n-antidipyramid, n-antibipyramid, or n-deltohedron, is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.
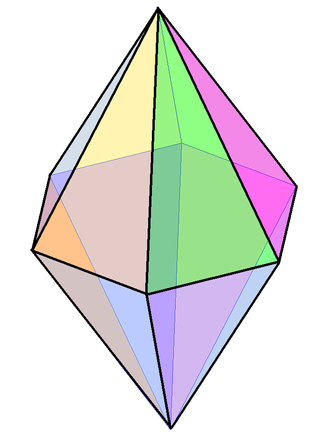
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.
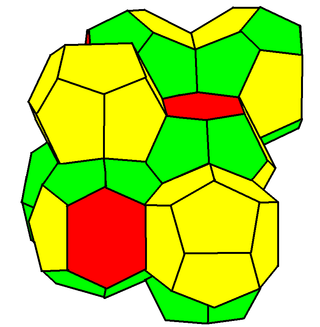
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure.

In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices.

In geometry, a decahedron is a polyhedron with ten faces. There are 32300 topologically distinct decahedra, and none are regular, so this name does not identify a specific type of polyhedron except for the number of faces.

In geometry, a trigonal trapezohedron is a polyhedron with six congruent quadrilateral faces, which may be scalene or rhomboid. The variety with rhombus-shaped faces faces is a rhombohedron. An alternative name for the same shape is the trigonal deltohedron.

In geometry, an n-gonaltruncated trapezohedron is a polyhedron formed by a n-gonal trapezohedron with n-gonal pyramids truncated from its two polar axis vertices.

In geometry, the square truncated trapezohedron is the second in an infinite series of truncated trapezohedra. It has 8 pentagon and 2 square faces.
In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.
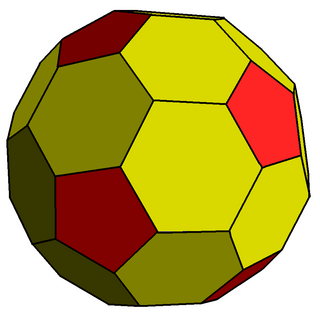
In geometry, the chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.
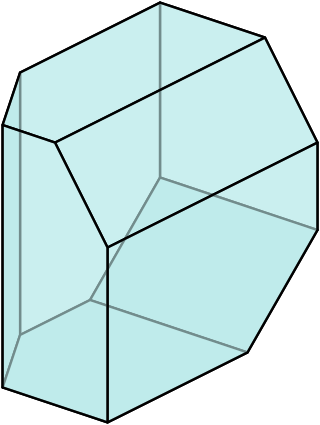
In geometry, a d-dimensional simple polytope is a d-dimensional polytope each of whose vertices are adjacent to exactly d edges (also d facets). The vertex figure of a simple d-polytope is a (d – 1)-simplex.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
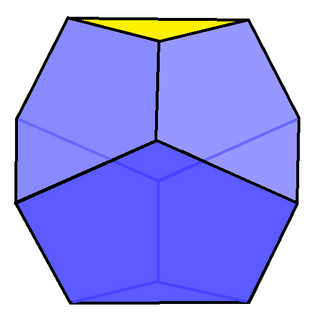
In geometry, the truncated triangular trapezohedron is the first in an infinite series of truncated trapezohedra. It has 6 pentagon and 2 triangle faces.