Related Research Articles
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.
In 3D computer graphics, solid objects are usually modeled by polyhedra. A face of a polyhedron is a planar polygon bounded by straight line segments, called edges. Curved surfaces are usually approximated by a polygon mesh. Computer programs for line drawings of opaque objects must be able to decide which edges or which parts of the edges are hidden by an object itself or by other objects, so that those edges can be clipped during rendering. This problem is known as hidden-line removal.
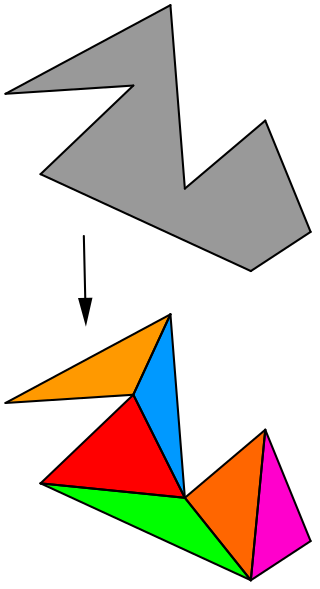
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.
In computational geometry and robot motion planning, a visibility graph is a graph of intervisible locations, typically for a set of points and obstacles in the Euclidean plane. Each node in the graph represents a point location, and each edge represents a visible connection between them. That is, if the line segment connecting two locations does not pass through any obstacle, an edge is drawn between them in the graph. When the set of locations lies in a line, this can be understood as an ordered series. Visibility graphs have therefore been extended to the realm of time series analysis.
The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:
"In an art gallery, what is the minimum number of guards who together can observe the whole gallery?"

In geometry, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction as C at these points. That is, L is a tangent line at P and at Q.
Motion planning, also path planning is a computational problem to find a sequence of valid configurations that moves the object from the source to destination. The term is used in computational geometry, computer animation, robotics and computer games.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles.

In computational geometry, the visibility polygon or visibility region for a point p in the plane among obstacles is the possibly unbounded polygonal region of all points of the plane visible from p. The visibility polygon can also be defined for visibility from a segment, or a polygon. Visibility polygons are useful in robotics, video games, and in various optimization problems such as the facility location problem and the art gallery problem.

In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
John E. Hershberger is an American computer scientist and software professional, a principal engineer at Mentor Graphics Corporation since 1993. He is known for his research in computational geometry and algorithm engineering.
Art Gallery Theorems and Algorithms is a mathematical monograph on topics related to the art gallery problem, on finding positions for guards within a polygonal museum floorplan so that all points of the museum are visible to at least one guard, and on related problems in computational geometry concerning polygons. It was written by Joseph O'Rourke, and published in 1987 in the International Series of Monographs on Computer Science of the Oxford University Press. Only 1000 copies were produced before the book went out of print, so to keep this material accessible O'Rourke has made a pdf version of the book available online.
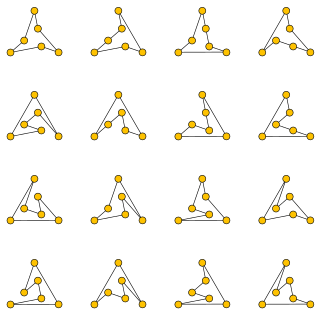
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.
References
- O'Rourke, Joseph (1987). Art Gallery Theorems and Algorithms. Oxford University Press. ISBN 0-19-503965-3.
- Ghosh, Subir Kumar (2007). Visibility Algorithms in the Plane. Cambridge University Press. ISBN 978-0-521-87574-5.
- Mark de Berg, Marc van Kreveld, Mark Overmars, and Otfried Schwarzkopf (2000). Computational Geometry (2nd revised ed.). Springer-Verlag. ISBN 3-540-65620-0. 1st edition (1987).
{{cite book}}: CS1 maint: multiple names: authors list (link) Chapter 15: "Visibility graphs"
- ↑ D. Avis and G. T. Toussaint, "An optimal algorithm for determining the visibility of a polygon from an edge," IEEE Transactions on Computers, vol. C-30, No. 12, December 1981, pp. 910-914.
- ↑ E. Roth, G. Panin and A. Knoll, "Sampling feature points for contour tracking with graphics hardware", "In International Workshop on Vision, Modeling and Visualization (VMV)", Konstanz, Germany, October 2008.