In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a homotopy invariant—topological spaces that are homotopy equivalent have isomorphic fundamental groups. The fundamental group of a topological space is denoted by .
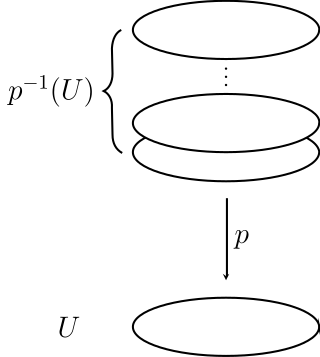
In topology, a covering or covering projection is a surjective map between topological spaces that, intuitively, locally acts like a projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If is a covering, is said to be a covering space or cover of , and is said to be the base of the covering, or simply the base. By abuse of terminology, and may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étale space.
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics.
In mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism. The theorem is named after Witold Hurewicz, and generalizes earlier results of Henri Poincaré.
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group. These concepts are named after the mathematician J. H. C. Whitehead.
In mathematics, particularly algebraic topology, cohomotopy sets are particular contravariant functors from the category of pointed topological spaces and basepoint-preserving continuous maps to the category of sets and functions. They are dual to the homotopy groups, but less studied.
In mathematics, the Ext functors are the derived functors of the Hom functor. Along with the Tor functor, Ext is one of the core concepts of homological algebra, in which ideas from algebraic topology are used to define invariants of algebraic structures. The cohomology of groups, Lie algebras, and associative algebras can all be defined in terms of Ext. The name comes from the fact that the first Ext group Ext1 classifies extensions of one module by another.
In mathematics, specifically algebraic topology, an Eilenberg–MacLane space is a topological space with a single nontrivial homotopy group.

In mathematics, specifically in algebraic geometry, the Grothendieck–Riemann–Roch theorem is a far-reaching result on coherent cohomology. It is a generalisation of the Hirzebruch–Riemann–Roch theorem, about complex manifolds, which is itself a generalisation of the classical Riemann–Roch theorem for line bundles on compact Riemann surfaces.
In mathematics, and especially in homotopy theory, a crossed module consists of groups and , where acts on by automorphisms (which we will write on the left, , and a homomorphism of groups
In algebraic topology, a Steenrod algebra was defined by Henri Cartan (1955) to be the algebra of stable cohomology operations for mod cohomology.
In mathematics, the J-homomorphism is a mapping from the homotopy groups of the special orthogonal groups to the homotopy groups of spheres. It was defined by George W. Whitehead (1942), extending a construction of Heinz Hopf (1935).
In mathematics, in particular in algebraic topology, the Hopf invariant is a homotopy invariant of certain maps between n-spheres.
In mathematics, the Toda bracket is an operation on homotopy classes of maps, in particular on homotopy groups of spheres, named after Hiroshi Toda, who defined them and used them to compute homotopy groups of spheres in.
In mathematics and specifically in topology, rational homotopy theory is a simplified version of homotopy theory for topological spaces, in which all torsion in the homotopy groups is ignored. It was founded by Dennis Sullivan (1977) and Daniel Quillen (1969). This simplification of homotopy theory makes certain calculations much easier.
In mathematics, Reidemeister torsion is a topological invariant of manifolds introduced by Kurt Reidemeister for 3-manifolds and generalized to higher dimensions by Wolfgang Franz (1935) and Georges de Rham (1936). Analytic torsion is an invariant of Riemannian manifolds defined by Daniel B. Ray and Isadore M. Singer as an analytic analogue of Reidemeister torsion. Jeff Cheeger and Werner Müller (1978) proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.
In homotopy theory, a branch of algebraic topology, a Postnikov system is a way of decomposing a topological space's homotopy groups using an inverse system of topological spaces whose homotopy type at degree agrees with the truncated homotopy type of the original space . Postnikov systems were introduced by, and are named after, Mikhail Postnikov.
In the mathematical surgery theory the surgery exact sequence is the main technical tool to calculate the surgery structure set of a compact manifold in dimension . The surgery structure set of a compact -dimensional manifold is a pointed set which classifies -dimensional manifolds within the homotopy type of .
This is a glossary of properties and concepts in algebraic topology in mathematics.
The Whitehead product is a mathematical construction introduced in Whitehead (1941). It has been a useful tool in determining the properties of spaces. The mathematical notion of space includes every shape that exists in our 3-dimensional world such as curves, surfaces, and solid figures. Since spaces are often presented by formulas, it is usually not possible to visually determine their geometric properties. Some of these properties are connectedness, the number of holes the space has, the knottedness of the space, and so on. Spaces are then studied by assigning algebraic constructions to them. This is similar to what is done in high school analytic geometry whereby to certain curves in the plane are assigned equations. The most common algebraic constructions are groups. These are sets such that any two members of the set can be combined to yield a third member of the set. In homotopy theory, one assigns a group to each space X and positive integer p called the pth homotopy group of X. These groups have been studied extensively and give information about the properties of the space X. There are then operations among these groups which provide additional information about the spaces. This has been very important in the study of homotopy groups.








































