Xuong tree

Last updated February 24, 2019

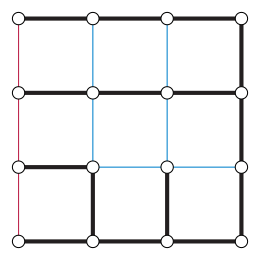
In graph theory, a Xuong tree is a spanning tree $T$ of a given graph $G$ with the property that, in the remaining graph $G-T$ , the number of connected components with an odd number of edges is as small as possible.^[1] They are named after Nguyen Huy Xuong, who used them to characterize the cellular embeddings of a given graph having the largest possible genus.^[2]

Graph theory study of graphs, which are mathematical structures used to model pairwise relations between objects

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices, nodes, or points which are connected by edges, arcs, or lines. A graph may be undirected, meaning that there is no distinction between the two vertices associated with each edge, or its edges may be directed from one vertex to another; see Graph for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G, with minimum possible number of edges. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

Connected component (graph theory) maximal subgraph of a given node-link graph within which every two vertices may be connected by a path

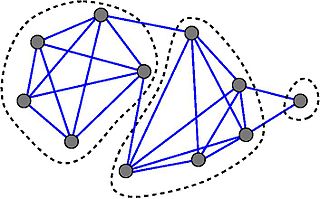
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices in the supergraph. For example, the graph shown in the illustration has three connected components. A vertex with no incident edges is itself a connected component. A graph that is itself connected has exactly one connected component, consisting of the whole graph.

According to Xuong's results, if $T$ is a Xuong tree and the numbers of edges in the components of $G-T$ are $m_{1},m_{2},\dots ,m_{k}$ , then the maximum genus of an embedding of $G$ is $\textstyle \sum _{i=1}^{k}\lfloor m_{i}/2\rfloor$ .^[1]^[2] Any one of these components, having $m_{i}$ edges, can be partitioned into $\lfloor m_{i}/2\rfloor$ edge-disjoint two-edge paths, with possibly one additional left-over edge.^[3] An embedding of maximum genus may be obtained from a planar embedding of the Xuong tree by adding each two-edge path to the embedding in such a way that it increases the genus by one.^[1]^[2]

A Xuong tree, and a maximum-genus embedding derived from it, may be found in any graph in polynomial time, by a transformation to a more general computational problem on matroids, the matroid parity problem for linear matroids.^[1]^[4]

In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid, the most significant being in terms of independent sets, bases, circuits, closed sets or flats, closure operators, and rank functions.

In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.

Related Research Articles

The Turán graphT(n,r) is a complete multipartite graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge if and only if they belong to different subsets. The graph will have $subsets of size, and subsets of size . That is, it is a complete r -partite graph$

In graph theory, Turán's theorem is a result on the number of edges in a K_r+1-free graph.

In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is called a planar matroid; these are exactly the graphic matroids formed from planar graphs.

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. For surfaces of genus 0, 1, 2, 3, 4, 5, 6, 7, ..., the required number of colors is 4, 7, 8, 9, 10, 11, 12, 12, .... OEIS: A000934, the chromatic number or Heawood number.

The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph.

In the mathematical discipline of graph theory, the dual graph of a plane graph $G$ is a graph that has a vertex for each face of $G$ . The dual graph has an edge whenever two faces of $G$ are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge $e$ of $G$ has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of $e$ . The definition of the dual depends on the choice of embedding of the graph $G$ , so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In mathematics, the Cheeger constant of a graph is a numerical measure of whether or not a graph has a "bottleneck". The Cheeger constant as a measure of "bottleneckedness" is of great interest in many areas: for example, constructing well-connected networks of computers, card shuffling. The graph theoretical notion originated after the Cheeger isoperimetric constant of a compact Riemannian manifold.

In graph theory, a peripheral cycle in an undirected graph is, intuitively, a cycle that does not separate any part of the graph from any other part. Peripheral cycles were first studied by Tutte (1963), and play important roles in the characterization of planar graphs and in generating the cycle spaces of nonplanar graphs.

In the mathematical subject of matroid theory, the bicircular matroid of a graph G is the matroid B(G) whose points are the edges of G and whose independent sets are the edge sets of pseudoforests of G, that is, the edge sets in which each connected component contains at most one cycle.

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have at most k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the two-graph clique-sum operation.

In the branch of mathematics called graph theory, the strength of an undirected graph corresponds to the minimum ratio edges removed/components created in a decomposition of the graph in question. It is a method to compute partitions of the set of vertices and detect zones of high concentration of edges, and is analogous to graph toughness which is defined similarly for vertex removal.

In the mathematical discipline of graph theory, Shannon multigraphs, named after Claude Shannon by Vizing (1965), are a special type of triangle graphs, which are used in the field of edge coloring in particular.

In matroid theory, a field within mathematics, a gammoid is a certain kind of matroid, describing sets of vertices that can be reached by vertex-disjoint paths in a directed graph.

In graph theory, the graph bandwidth problem is to label the n vertices v_i of a graph G with distinct integers f(v_i) so that the quantity $is minimized . The problem may be visualized as placing the vertices of a graph at distinct integer points along the x -axis so that the length of the longest edge is minimized. Such placement is called linear graph arrangement, linear graph layout or linear graph placement .$

In the mathematics of structural rigidity, a rigidity matroid is a matroid that describes the number of degrees of freedom of an undirected graph with rigid edges of fixed lengths, embedded into Euclidean space. In a rigidity matroid for a graph with n vertices in d-dimensional space, a set of edges that defines a subgraph with k degrees of freedom has matroid rank dn − k. A set of edges is independent if and only if, for every edge in the set, removing the edge would increase the number of degrees of freedom of the remaining subgraph.

In graph theory, a branch of mathematics, the kth powerG^k of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G² is called the square of G, G³ is called the cube of G, etc.

References

1 2 3 4 Beineke, Lowell W.; Wilson, Robin J. (2009), Topics in topological graph theory, Encyclopedia of Mathematics and its Applications, 128, Cambridge University Press, Cambridge, p. 36, doi:10.1017/CBO9781139087223, ISBN 978-0-521-80230-7, MR 2581536
1 2 3 Xuong, Nguyen Huy (1979), "How to determine the maximum genus of a graph", Journal of Combinatorial Theory, Series B, 26 (2): 217–225, doi:10.1016/0095-8956(79)90058-3, MR 0532589
↑ Sumner, David P. (1974), "Graphs with 1-factors", Proceedings of the American Mathematical Society, American Mathematical Society, 42 (1): 8–12, doi:10.2307/2039666, JSTOR 2039666, MR 0323648
↑ Furst, Merrick L.; Gross, Jonathan L.; McGeoch, Lyle A. (1988), "Finding a maximum-genus graph imbedding", Journal of the ACM , 35 (3): 523–534, doi:10.1145/44483.44485, MR 0963159

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[bw-1] 1 2 3 4 Beineke, Lowell W.; Wilson, Robin J. (2009), Topics in topological graph theory, Encyclopedia of Mathematics and its Applications, 128, Cambridge University Press, Cambridge, p. 36, doi:10.1017/CBO9781139087223, ISBN 978-0-521-80230-7, MR 2581536

[x-2] 1 2 3 Xuong, Nguyen Huy (1979), "How to determine the maximum genus of a graph", Journal of Combinatorial Theory, Series B, 26 (2): 217–225, doi:10.1016/0095-8956(79)90058-3, MR 0532589

[s-3] Sumner, David P. (1974), "Graphs with 1-factors", Proceedings of the American Mathematical Society, American Mathematical Society, 42 (1): 8–12, doi:10.2307/2039666, JSTOR 2039666, MR 0323648

[fgm-4] Furst, Merrick L.; Gross, Jonathan L.; McGeoch, Lyle A. (1988), "Finding a maximum-genus graph imbedding", Journal of the ACM , 35 (3): 523–534, doi:10.1145/44483.44485, MR 0963159