Spontaneous emission is the process in which a quantum mechanical system transits from an excited energy state to a lower energy state and emits a quantized amount of energy in the form of a photon. Spontaneous emission is ultimately responsible for most of the light we see all around us; it is so ubiquitous that there are many names given to what is essentially the same process. If atoms are excited by some means other than heating, the spontaneous emission is called luminescence. For example, fireflies are luminescent. And there are different forms of luminescence depending on how excited atoms are produced. If the excitation is affected by the absorption of radiation the spontaneous emission is called fluorescence. Sometimes molecules have a metastable level and continue to fluoresce long after the exciting radiation is turned off; this is called phosphorescence. Figurines that glow in the dark are phosphorescent. Lasers start via spontaneous emission, then during continuous operation work by stimulated emission.
The Mössbauer effect, or recoilless nuclear resonance fluorescence, is a physical phenomenon discovered by Rudolf Mössbauer in 1958. It involves the resonant and recoil-free emission and absorption of gamma radiation by atomic nuclei bound in a solid. Its main application is in Mössbauer spectroscopy.

Photoluminescence is light emission from any form of matter after the absorption of photons. It is one of many forms of luminescence and is initiated by photoexcitation, hence the prefix photo-. Following excitation, various relaxation processes typically occur in which other photons are re-radiated. Time periods between absorption and emission may vary: ranging from short femtosecond-regime for emission involving free-carrier plasma in inorganic semiconductors up to milliseconds for phosphoresence processes in molecular systems; and under special circumstances delay of emission may even span to minutes or hours.

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. Often referred to as a quasiparticle, it is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves.
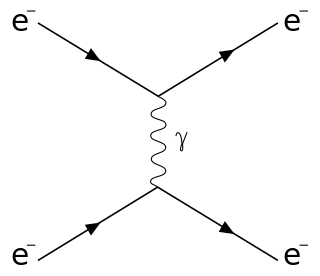
Raman scattering or the Raman effect is the inelastic scattering of photons by matter, meaning that there is both an exchange of energy and a change in the light's direction. Typically this effect involves vibrational energy being gained by a molecule as incident photons from a visible laser are shifted to lower energy. This is called normal Stokes Raman scattering. The effect is exploited by chemists and physicists to gain information about materials for a variety of purposes by performing various forms of Raman spectroscopy. Many other variants of Raman spectroscopy allow rotational energy to be examined and electronic energy levels may be examined if an X-ray source is used in addition to other possibilities. More complex techniques involving pulsed lasers, multiple laser beams and so on are known.

A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933 and Solomon Pekar in 1946 to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. For comparison of the models proposed in these papers see M. I. Dykman and E. I. Rashba, The roots of polaron theory, Physics Today 68, 10 (2015). This lowers the electron mobility and increases the electron's effective mass.
Resolved sideband cooling is a laser cooling technique allowing cooling of tightly bound atoms and ions beyond the Doppler cooling limit, potentially to their motional ground state. Aside from the curiosity of having a particle at zero point energy, such preparation of a particle in a definite state with high probability (initialization) is an essential part of state manipulation experiments in quantum optics and quantum computing.
Resonance Raman spectroscopy is a Raman spectroscopy technique in which the incident photon energy is close in energy to an electronic transition of a compound or material under examination. The frequency coincidence can lead to greatly enhanced intensity of the Raman scattering, which facilitates the study of chemical compounds present at low concentrations.

According to quantum mechanics, atoms and molecules can only hold certain defined quantities of energy, or exist in specific states. When such quanta of electromagnetic radiation are emitted or absorbed by an atom or molecule, energy of the radiation changes the state of the atom or molecule from an initial state to a final state. An absorption band is a range of wavelengths, frequencies or energies in the electromagnetic spectrum which are characteristic of a particular transition from initial to final state in a substance.
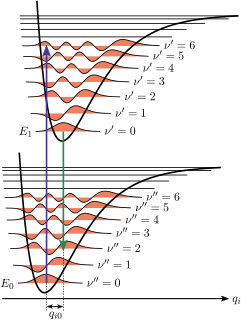
The Franck–Condon principle is a rule in spectroscopy and quantum chemistry that explains the intensity of vibronic transitions. Vibronic transitions are the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. The principle states that during an electronic transition, a change from one vibrational energy level to another will be more likely to happen if the two vibrational wave functions overlap more significantly.

Sound amplification by stimulated emission of radiation (SASER) refers to a device that emits acoustic radiation. It focuses sound waves in a way that they can serve as accurate and high-speed carriers of information in many kinds of applications—similar to uses of laser light.

Shpolskii systems are low-temperature host–guest systems – they are typically rapidly frozen solutions of polycyclic aromatic hydrocarbons in suitable low molecular weight normal alkanes. The emission and absorption spectra of lowest energy electronic transitions in the Shpolskii systems exhibit narrow lines instead of the inhomogeneously broadened features normally associated with spectra of chromophores in liquids and amorphous solids. The effect was first described by Eduard Shpolskii in the 1950s and 1960's in the journals Transactions of the U.S.S.R. Academy of Sciences and Soviet Physics Uspekhi.
The McCumber relation is a relationship between the effective cross-sections of absorption and emission of light in the physics of solid-state lasers. It is named after Dean McCumber, who proposed the relationship in 1964.

In solid state physics, a surface phonon is the quantum of a lattice vibration mode associated with a solid surface. Similar to the ordinary lattice vibrations in a bulk solid, the nature of surface vibrations depends on details of periodicity and symmetry of a crystal structure. Surface vibrations are however distinct from the bulk vibrations, as they arise from the abrupt termination of a crystal structure at the surface of a solid. Knowledge of surface phonon dispersion gives important information related to the amount of surface relaxation, the existence and distance between an adsorbate and the surface, and information regarding presence, quantity, and type of defects existing on the surface.
Free carrier absorption occurs when a material absorbs a photon, and a carrier is excited from an already-excited state to another, unoccupied state in the same band. This intraband absorption is different from interband absorption because the excited carrier is already in an excited band, such as an electron in the conduction band or a hole in the valence band, where it is free to move. In interband absorption, the carrier starts in a fixed, nonconducting band and is excited to a conducting one.

In condensed matter physics, the Lyddane–Sachs–Teller relation determines the ratio of the natural frequency of longitudinal optic lattice vibrations (phonons) of an ionic crystal to the natural frequency of the transverse optical lattice vibration for long wavelengths. The ratio is that of the static permittivity to the permittivity for frequencies in the visible range .
The quasi-harmonic approximation is a phonon-based model of solid-state physics used to describe volume-dependent thermal effects, such as the thermal expansion. It is based on the assumption that the harmonic approximation holds for every value of the lattice constant, which is to be viewed as an adjustable parameter.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.
Vibronic spectroscopy is a branch of molecular spectroscopy concerned with vibronic transitions: the simultaneous changes in electronic and vibrational energy levels of a molecule due to the absorption or emission of a photon of the appropriate energy. In the gas phase vibronic transitions are accompanied by changes in rotational energy also. Vibronic spectra of diatomic molecules have been analysed in detail; emission spectra are more complicated than absorption spectra. The intensity of allowed vibronic transitions is governed by the Franck–Condon principle. Vibronic spectroscopy may provide information, such as bond-length, on electronic excited states of stable molecules. It has also been applied to the study of unstable molecules such as dicarbon, C2, in discharges, flames and astronomical objects.
The semiconductor luminescence equations (SLEs) describe luminescence of semiconductors resulting from spontaneous recombination of electronic excitations, producing a flux of spontaneously emitted light. This description established the first step toward semiconductor quantum optics because the SLEs simultaneously includes the quantized light–matter interaction and the Coulomb-interaction coupling among electronic excitations within a semiconductor. The SLEs are one of the most accurate methods to describe light emission in semiconductors and they are suited for a systematic modeling of semiconductor emission ranging from excitonic luminescence to lasers.


















