The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields – as they occur in classical physics – such as mechanical waves or electromagnetic waves. It arises in fields like acoustics, electromagnetism, and fluid dynamics. Single mechanical or electromagnetic waves propagating in a pre-defined direction can also be described with the first-order one-way wave equation, which is much easier to solve and also valid for inhomogeneous media.
The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.

In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.
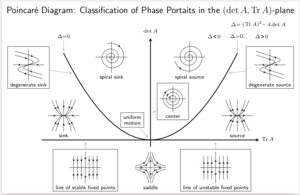
In the theory of ordinary differential equations (ODEs), Lyapunov functions, named after Aleksandr Lyapunov, are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Lyapunov functions are important to stability theory of dynamical systems and control theory. A similar concept appears in the theory of general state space Markov chains, usually under the name Foster–Lyapunov functions.
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form

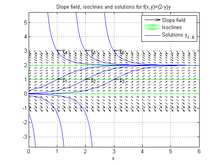
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.

In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively.
In mathematics and its applications, classical Sturm–Liouville theory is the theory of real second-order linear ordinary differential equations of the form:

In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation. The method is to reduce a partial differential equation to a family of ordinary differential equations along which the solution can be integrated from some initial data given on a suitable hypersurface.
In mathematics, an Euler–Cauchy equation, or Cauchy–Euler equation, or simply Euler's equation is a linear homogeneous ordinary differential equation with variable coefficients. It is sometimes referred to as an equidimensional equation. Because of its particularly simple equidimensional structure, the differential equation can be solved explicitly.

In mathematics, the method of undetermined coefficients is an approach to finding a particular solution to certain nonhomogeneous ordinary differential equations and recurrence relations. It is closely related to the annihilator method, but instead of using a particular kind of differential operator in order to find the best possible form of the particular solution, an ansatz or 'guess' is made as to the appropriate form, which is then tested by differentiating the resulting equation. For complex equations, the annihilator method or variation of parameters is less time-consuming to perform.

In mathematics, an integrating factor is a function that is chosen to facilitate the solving of a given equation involving differentials. It is commonly used to solve ordinary differential equations, but is also used within multivariable calculus when multiplying through by an integrating factor allows an inexact differential to be made into an exact differential. This is especially useful in thermodynamics where temperature becomes the integrating factor that makes entropy an exact differential.

In mathematics, an exact differential equation or total differential equation is a certain kind of ordinary differential equation which is widely used in physics and engineering.
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with functions of other variables. The intent is that when expressed in new variables, the problem may become simpler, or equivalent to a better understood problem.
In mathematics, delay differential equations (DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times. DDEs are also called time-delay systems, systems with aftereffect or dead-time, hereditary systems, equations with deviating argument, or differential-difference equations. They belong to the class of systems with the functional state, i.e. partial differential equations (PDEs) which are infinite dimensional, as opposed to ordinary differential equations (ODEs) having a finite dimensional state vector. Four points may give a possible explanation of the popularity of DDEs:
- Aftereffect is an applied problem: it is well known that, together with the increasing expectations of dynamic performances, engineers need their models to behave more like the real process. Many processes include aftereffect phenomena in their inner dynamics. In addition, actuators, sensors, and communication networks that are now involved in feedback control loops introduce such delays. Finally, besides actual delays, time lags are frequently used to simplify very high order models. Then, the interest for DDEs keeps on growing in all scientific areas and, especially, in control engineering.
- Delay systems are still resistant to many classical controllers: one could think that the simplest approach would consist in replacing them by some finite-dimensional approximations. Unfortunately, ignoring effects which are adequately represented by DDEs is not a general alternative: in the best situation, it leads to the same degree of complexity in the control design. In worst cases, it is potentially disastrous in terms of stability and oscillations.
- Voluntary introduction of delays can benefit the control system.
- In spite of their complexity, DDEs often appear as simple infinite-dimensional models in the very complex area of partial differential equations (PDEs).
A differential equation can be homogeneous in either of two respects.

In differential calculus, there is no single uniform notation for differentiation. Instead, various notations for the derivative of a function or variable have been proposed by various mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation are listed below.
This is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus.
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders. A matrix differential equation contains more than one function stacked into vector form with a matrix relating the functions to their derivatives.
In applied mathematics and mathematical analysis, the fractal derivative or Hausdorff derivative is a non-Newtonian generalization of the derivative dealing with the measurement of fractals, defined in fractal geometry. Fractal derivatives were created for the study of anomalous diffusion, by which traditional approaches fail to factor in the fractal nature of the media. A fractal measure t is scaled according to tα. Such a derivative is local, in contrast to the similarly applied fractional derivative. Fractal calculus is formulated as a generalized of standard calculus