Binary decision diagram

"Branching program" redirects here. For other uses, see NC (complexity) § Barrington's theorem.

In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression.

Similar data structures include negation normal form (NNF), Zhegalkin polynomials, and propositional directed acyclic graphs (PDAG).

Definition

A Boolean function can be represented as a rooted, directed, acyclic graph, which consists of several (decision) nodes and two terminal nodes. The two terminal nodes are labeled 0 (FALSE) and 1 (TRUE). Each (decision) node ${\displaystyle u}$ is labeled by a Boolean variable ${\displaystyle x_{i}}$ and has two child nodes called low child and high child. The edge from node ${\displaystyle u}$ to a low (or high) child represents an assignment of the value FALSE (or TRUE, respectively) to variable ${\displaystyle x_{i}}$. Such a BDD is called 'ordered' if different variables appear in the same order on all paths from the root. A BDD is said to be 'reduced' if the following two rules have been applied to its graph:

• Merge any isomorphic subgraphs.
• Eliminate any node whose two children are isomorphic.

In popular usage, the term BDD almost always refers to Reduced Ordered Binary Decision Diagram (ROBDD in the literature, used when the ordering and reduction aspects need to be emphasized). The advantage of an ROBDD is that it is canonical (unique) for a particular function and variable order. ^[1] This property makes it useful in functional equivalence checking and other operations like functional technology mapping.

A path from the root node to the 1-terminal represents a (possibly partial) variable assignment for which the represented Boolean function is true. As the path descends to a low (or high) child from a node, then that node's variable is assigned to 0 (respectively 1).

Example

The left figure below shows a binary decision tree (the reduction rules are not applied), and a truth table, each representing the function ${\displaystyle f(x_{1},x_{2},x_{3})}$. In the tree on the left, the value of the function can be determined for a given variable assignment by following a path down the graph to a terminal. In the figures below, dotted lines represent edges to a low child, while solid lines represent edges to a high child. Therefore, to find ${\displaystyle f(0,1,1)}$, begin at x₁, traverse down the dotted line to x₂ (since x₁ has an assignment to 0), then down two solid lines (since x₂ and x₃ each have an assignment to one). This leads to the terminal 1, which is the value of ${\displaystyle f(0,1,1)}$.

The binary decision tree of the left figure can be transformed into a binary decision diagram by maximally reducing it according to the two reduction rules. The resulting BDD is shown in the right figure.

Binary decision tree and truth table for the function ${\displaystyle f(x_{1},x_{2},x_{3})=(\neg x_{1}\wedge \neg x_{2}\wedge \neg x_{3})\vee (x_{1}\wedge x_{2})\vee (x_{2}\wedge x_{3})}$, described in notation for Boolean operators.

BDD for the function f

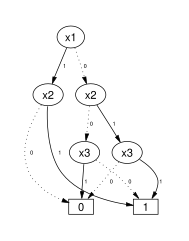Another notation for writing this Boolean function is ${\displaystyle {\overline {x}}_{1}{\overline {x}}_{2}{\overline {x}}_{3}+x_{1}x_{2}+x_{2}x_{3}}$.

Complemented edges

Representation of a binary decision diagram using complemented edges

An ROBDD can be represented even more compactly, using complemented edges. ^{[2] [3]} Complemented edges are formed by annotating low edges as complemented or not. If an edge is complemented, then it refers to the negation of the Boolean function that corresponds to the node that the edge points to (the Boolean function represented by the BDD with root that node). High edges are not complemented, in order to ensure that the resulting BDD representation is a canonical form. In this representation, BDDs have a single leaf node, for reasons explained below.

Two advantages of using complemented edges when representing BDDs are:

• computing the negation of a BDD takes constant time
• space usage (i.e., required memory) is reduced

A reference to a BDD in this representation is a (possibly complemented) "edge" that points to the root of the BDD. This is in contrast to a reference to a BDD in the representation without use of complemented edges, which is the root node of the BDD. The reason why a reference in this representation needs to be an edge is that for each Boolean function, the function and its negation are represented by an edge to the root of a BDD, and a complemented edge to the root of the same BDD. This is why negation takes constant time. It also explains why a single leaf node suffices: FALSE is represented by a complemented edge that points to the leaf node, and TRUE is represented by an ordinary edge (i.e., not complemented) that points to the leaf node.

For example, assume that a Boolean function is represented with a BDD represented using complemented edges. To find the value of the Boolean function for a given assignment of (Boolean) values to the variables, we start at the reference edge, which points to the BDD's root, and follow the path that is defined by the given variable values (following a low edge if the variable that labels a node equals FALSE, and following the high edge if the variable that labels a node equals TRUE), until we reach the leaf node. While following this path, we count how many complemented edges we have traversed. If when we reach the leaf node we have crossed an odd number of complemented edges, then the value of the Boolean function for the given variable assignment is FALSE, otherwise (if we have crossed an even number of complemented edges), then the value of the Boolean function for the given variable assignment is TRUE.

An example diagram of a BDD in this representation is shown on the right, and represents the same Boolean expression as shown in diagrams above, i.e., ${\displaystyle (\neg x_{1}\wedge \neg x_{2}\wedge \neg x_{3})\vee (x_{1}\wedge x_{2})\vee (x_{2}\wedge x_{3})}$. Low edges are dashed, high edges solid, and complemented edges are signified by a circle at their source. The node with the @ symbol represents the reference to the BDD, i.e., the reference edge is the edge that starts from this node.

History

The basic idea from which the data structure was created is the Shannon expansion. A switching function is split into two sub-functions (cofactors) by assigning one variable (cf. if-then-else normal form). If such a sub-function is considered as a sub-tree, it can be represented by a binary decision tree . Binary decision diagrams (BDDs) were introduced by C. Y. Lee, ^[4] and further studied and made known by Sheldon B. Akers ^[5] and Raymond T. Boute. ^[6] Independently of these authors, a BDD under the name "canonical bracket form" was realized Yu. V. Mamrukov in a CAD for analysis of speed-independent circuits. ^[7] The full potential for efficient algorithms based on the data structure was investigated by Randal Bryant at Carnegie Mellon University: his key extensions were to use a fixed variable ordering (for canonical representation) and shared sub-graphs (for compression). Applying these two concepts results in an efficient data structure and algorithms for the representation of sets and relations. ^{[8] [9]} By extending the sharing to several BDDs, i.e. one sub-graph is used by several BDDs, the data structure Shared Reduced Ordered Binary Decision Diagram is defined. ^[2] The notion of a BDD is now generally used to refer to that particular data structure.

In his video lecture Fun With Binary Decision Diagrams (BDDs), ^[10] Donald Knuth calls BDDs "one of the only really fundamental data structures that came out in the last twenty-five years" and mentions that Bryant's 1986 paper was for some time one of the most-cited papers in computer science.

Adnan Darwiche and his collaborators have shown that BDDs are one of several normal forms for Boolean functions, each induced by a different combination of requirements. Another important normal form identified by Darwiche is decomposable negation normal form or DNNF.

Applications

BDDs are extensively used in CAD software to synthesize circuits (logic synthesis) and in formal verification. There are several lesser known applications of BDD, including fault tree analysis, Bayesian reasoning, product configuration, and private information retrieval. ^{[11] [12] [ citation needed ]}

Every arbitrary BDD (even if it is not reduced or ordered) can be directly implemented in hardware by replacing each node with a 2 to 1 multiplexer; each multiplexer can be directly implemented by a 4-LUT in a FPGA. It is not so simple to convert from an arbitrary network of logic gates to a BDD^{[ citation needed ]} (unlike the and-inverter graph).

BDDs have been applied in efficient Datalog interpreters. ^[13]

Variable ordering

The size of the BDD is determined both by the function being represented and by the chosen ordering of the variables. There exist Boolean functions ${\displaystyle f(x_{1},\ldots ,x_{n})}$ for which depending upon the ordering of the variables we would end up getting a graph whose number of nodes would be linear (in n) at best and exponential at worst (e.g., a ripple carry adder). Consider the Boolean function ${\displaystyle f(x_{1},\ldots ,x_{2n})=x_{1}x_{2}+x_{3}x_{4}+\cdots +x_{2n-1}x_{2n}.}$ Using the variable ordering ${\displaystyle x_{1}<x_{3}<\cdots <x_{2n-1}<x_{2}<x_{4}<\cdots <x_{2n}}$, the BDD needs ${\displaystyle 2^{n+1}}$ nodes to represent the function. Using the ordering ${\displaystyle x_{1}<x_{2}<x_{3}<x_{4}<\cdots <x_{2n-1}<x_{2n}}$, the BDD consists of ${\displaystyle 2n+2}$ nodes.

BDD for the function ƒ(x1, ..., x8) = x1x2 + x3x4 + x5x6 + x7x8 using bad variable ordering

Good variable ordering

It is of crucial importance to care about variable ordering when applying this data structure in practice. The problem of finding the best variable ordering is NP-hard. ^[14] For any constant c > 1 it is even NP-hard to compute a variable ordering resulting in an OBDD with a size that is at most c times larger than an optimal one. ^[15] However, there exist efficient heuristics to tackle the problem. ^[16]

There are functions for which the graph size is always exponential—independent of variable ordering. This holds e.g. for the multiplication function. ^[1] In fact, the function computing the middle bit of the product of two ${\displaystyle n}$-bit numbers does not have an OBDD smaller than ${\displaystyle 2^{\lfloor n/2\rfloor }/61-4}$ vertices. ^[17] (If the multiplication function had polynomial-size OBDDs, it would show that integer factorization is in P/poly, which is not known to be true. ^[18] )

Researchers have suggested refinements on the BDD data structure giving way to a number of related graphs, such as BMD (binary moment diagrams), ZDD (zero-suppressed decision diagrams), FBDD (free binary decision diagrams), FDD (functional decision diagrams), PDD (parity decision diagrams), and MTBDDs (multiple terminal BDDs).

Logical operations on BDDs

Many logical operations on BDDs can be implemented by polynomial-time graph manipulation algorithms: ^{[19] : 20}

• conjunction
• disjunction
• negation

However, repeating these operations several times, for example forming the conjunction or disjunction of a set of BDDs, may in the worst case result in an exponentially big BDD. This is because any of the preceding operations for two BDDs may result in a BDD with a size proportional to the product of the BDDs' sizes, and consequently for several BDDs the size may be exponential in the number of operations. Variable ordering needs to be considered afresh; what may be a good ordering for (some of) the set of BDDs may not be a good ordering for the result of the operation. Also, since constructing the BDD of a Boolean function solves the NP-complete Boolean satisfiability problem and the co-NP-complete tautology problem, constructing the BDD can take exponential time in the size of the Boolean formula even when the resulting BDD is small.

Computing existential abstraction over multiple variables of reduced BDDs is NP-complete. ^[20]

Model-counting, counting the number of satisfying assignments of a Boolean formula, can be done in polynomial time for BDDs. For general propositional formulas the problem is ♯P-complete and the best known algorithms require an exponential time in the worst case.

See also

• Boolean satisfiability problem, the canonical NP-complete computational problem
• L/poly, a complexity class that strictly contains the set of problems with polynomially sized BDDs^{[ citation needed ]}
• Model checking
• Radix tree
• Barrington's theorem
• Hardware acceleration
• Karnaugh map, a method of simplifying Boolean algebra expressions
• Zero-suppressed decision diagram
• Algebraic decision diagram, a generalization of BDDs from two-element to arbitrary finite sets
• Sentential Decision Diagram, a generalization of OBDDs
• Influence diagram

References

1. Bryant, Randal E. (August 1986). "Graph-Based Algorithms for Boolean Function Manipulation" (PDF). IEEE Transactions on Computers. C-35 (8): 677–691. CiteSeerX   10.1.1.476.2952 . doi:10.1109/TC.1986.1676819. S2CID   10385726.
2. Brace, Karl S.; Rudell, Richard L.; Bryant, Randal E. (1990). "Efficient Implementation of a BDD Package". Proceedings of the 27th ACM/IEEE Design Automation Conference (DAC 1990). IEEE Computer Society Press. pp. 40–45. doi:10.1145/123186.123222. ISBN   978-0-89791-363-8.
3. Somenzi, Fabio (1999). "Binary decision diagrams" (PDF). Calculational system design. NATO Science Series F: Computer and systems sciences. Vol. 173. IOS Press. pp. 303–366. ISBN   978-90-5199-459-9.
4. Lee, C.Y. (1959). "Representation of Switching Circuits by Binary-Decision Programs". Bell System Technical Journal. 38 (4): 985–999. doi:10.1002/j.1538-7305.1959.tb01585.x.
5. Akers, Jr., Sheldon B (June 1978). "Binary Decision Diagrams". IEEE Transactions on Computers. C-27 (6): 509–516. doi:10.1109/TC.1978.1675141. S2CID   21028055.
6. Boute, Raymond T. (January 1976). "The Binary Decision Machine as a programmable controller". EUROMICRO Newsletter. 1 (2): 16–22. doi:10.1016/0303-1268(76)90033-X.
7. Mamrukov, Yu. V. (1984). Analysis of aperiodic circuits and asynchronous processes (PhD). Leningrad Electrotechnical Institute.
8. Bryant., Randal E. (1986). "Graph-Based Algorithms for Boolean Function Manipulation" (PDF). IEEE Transactions on Computers. C-35 (8): 677–691. doi:10.1109/TC.1986.1676819. S2CID   10385726.
9. Bryant, Randal E. (September 1992). "Symbolic Boolean Manipulation with Ordered Binary Decision Diagrams". ACM Computing Surveys. 24 (3): 293–318. doi:10.1145/136035.136043. S2CID   1933530.
10. "Stanford Center for Professional Development". scpd.stanford.edu. Archived from the original on 2014-06-04. Retrieved 2018-04-23.
11. Jensen, R.M. (2004). "CLab: A C++ library for fast backtrack-free interactive product configuration". Proceedings of the Tenth International Conference on Principles and Practice of Constraint Programming. Lecture Notes in Computer Science. Vol. 3258. Springer. p. 816. doi:10.1007/978-3-540-30201-8_94. ISBN   978-3-540-30201-8.
12. Lipmaa, H.L. (2009). "First CPIR Protocol with Data-Dependent Computation" (PDF). International Conference on Information Security and Cryptology. Lecture Notes in Computer Science. Vol. 5984. Springer. pp. 193–210. doi:10.1007/978-3-642-14423-3_14. ISBN   978-3-642-14423-3.
13. Whaley, John; Avots, Dzintars; Carbin, Michael; Lam, Monica S. (2005). "Using Datalog with Binary Decision Diagrams for Program Analysis". In Yi, Kwangkeun (ed.). Programming Languages and Systems. Lecture Notes in Computer Science. Vol. 3780. Berlin, Heidelberg: Springer. pp. 97–118. doi:10.1007/11575467_8. ISBN   978-3-540-32247-4. S2CID   5223577.
14. Bollig, Beate; Wegener, Ingo (September 1996). "Improving the Variable Ordering of OBDDs Is NP-Complete". IEEE Transactions on Computers. 45 (9): 993–1002. doi:10.1109/12.537122.
15. Sieling, Detlef (2002). "The nonapproximability of OBDD minimization". Information and Computation. 172 (2): 103–138. doi: 10.1006/inco.2001.3076 .
16. Rice, Michael. "A Survey of Static Variable Ordering Heuristics for Efficient BDD/MDD Construction" (PDF).
17. Woelfel, Philipp (2005). "Bounds on the OBDD-size of integer multiplication via universal hashing". Journal of Computer and System Sciences. 71 (4): 520–534. CiteSeerX   10.1.1.138.6771 . doi: 10.1016/j.jcss.2005.05.004 .
18. Richard J. Lipton. "BDD's and Factoring". Gödel's Lost Letter and P=NP, 2009.
19. Andersen, H. R. (1999). "An Introduction to Binary Decision Diagrams" (PDF). Lecture Notes. IT University of Copenhagen.
20. Huth, Michael; Ryan, Mark (2004). Logic in computer science: modelling and reasoning about systems (2nd ed.). Cambridge University Press. pp. 380–. ISBN   978-0-52154310-1. OCLC   54960031.

Further reading

• Ubar, R. (1976). "Test Generation for Digital Circuits Using Alternative Graphs". Proc. Tallinn Technical University (in Russian) (409). Tallinn, Estonia: 75–81.
• Knuth, D.E. (2009). Fascicle 1: Bitwise tricks & techniques; Binary Decision Diagrams. The Art of Computer Programming. Vol. 4. Addison–Wesley. ISBN   978-0-321-58050-4. Draft of Fascicle 1b Archived 2016-03-12 at the Wayback Machine available for download.
• Meinel, C.; Theobald, T. (2012) [1998]. Algorithms and Data Structures in VLSI-Design: OBDD – Foundations and Applications (PDF). Springer. ISBN   978-3-642-58940-9. Complete textbook available for download.
• Ebendt, Rüdiger; Fey, Görschwin; Drechsler, Rolf (2005). Advanced BDD optimization. Springer. ISBN   978-0-387-25453-1.
• Becker, Bernd; Drechsler, Rolf (1998). Binary Decision Diagrams: Theory and Implementation. Springer. ISBN   978-1-4419-5047-5.

External links

• Fun With Binary Decision Diagrams (BDDs), lecture by Donald Knuth
• List of BDD software libraries for several programming languages.