A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from Latin stella, "star". Stellation is the reciprocal or dual process to faceting.
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.

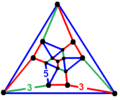
In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram. That is, every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron, or inside of it.

In geometry, the great stellated dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.

In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.
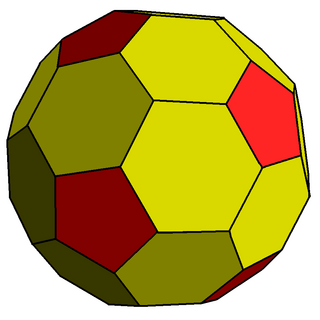
In geometry, the chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.

In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.

In geometry, faceting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.

In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty', and ἕδρα (hédra) 'seat'. The plural can be either "icosahedra" or "icosahedrons".