Fractal-generating software

Last updated
3D fractal made with Fragmentarium Fragmentarium.png
3D fractal made with Fragmentarium

Fractal-generating software is any type of graphics software that generates images of fractals. There are many fractal generating programs available, both free and commercial. Mobile apps are available to play or tinker with fractals. Some programmers create fractal software for themselves because of the novelty and because of the challenge in understanding the related mathematics. The generation of fractals has led to some very large problems for pure mathematics. [1]

Contents

Fractal generating software creates mathematical beauty through visualization. Modern computers may take seconds or minutes to complete a single high resolution fractal image. Images are generated for both simulation (modeling) and random fractals for art. Fractal generation used for modeling is part of realism in computer graphics. [2] Fractal generation software can be used to mimic natural landscapes with fractal landscapes and scenery generation programs. Fractal imagery can be used to introduce irregularity to an otherwise sterile computer generated environment. [3]

Simple Koch curves display strict self-similarity Fractal koch.png
Simple Koch curves display strict self-similarity

Fractals are generated in music visualization software, screensavers and wallpaper generators. This software presents the user with a more limited range of settings and features, sometimes relying a series pre-programmed variables. Because complex images can be generated from simple formula fractals are often used among the demoscene. [4] The generation of fractals such as the Mandelbrot set is time-consuming and requires many computations, so it is often used in benchmarking devices. [5]

History

A similar plot to the very first render by Benoit Mandelbrot Centers8.png
A similar plot to the very first render by Benoit Mandelbrot
Palette editor in Fractint Mandelbrot palette colour editing with Fractint.png
Palette editor in Fractint

The generation of fractals by calculation without computer assistance was undertaken by German mathematician Georg Cantor in 1883 to create the Cantor set. [6] Throughout the following years, mathematicians have postulated the existence of numerous fractals. Some were conceived before the naming of fractals in 1975, for example, the Pythagoras tree by Dutch mathematics teacher Albert E. Bosman in 1942.

The development of the first fractal generating software originated in Benoit Mandelbrot's pursuit of a generalized function for a class of shapes known as Julia sets. In 1979, Mandelbrot discovered that one image of the complex plane could be created by iteration. He and programmers working at IBM generated the first rudimentary fractal printouts. [7] This marked the first instance of the generation of fractals by non-linear creations laws or 'escape time fractal'. [8] [9] Loren Carpenter created a two-minute color film called Vol Libre for presentation at SIGGRAPH in 1980. [10] The October 1983 issue of Acorn User magazine carried a BBC BASIC listing for generating fractal shapes by Susan Stepney, now Professor of Computer Science at the University of York. [11] [12] She followed this up in the March 1984 Acorn User with “Snowflakes and other fractal monsters”. [13] Fractals were rendered in computer games as early as 1984 with the creation of Rescue on Fractalus! . From the early 1980s to about 1995 hundreds of different fractal types were formulated. [14]

The generation of fractal images grew in popularity as the distribution of computers with a maths co-processor or floating-point unit in the central processing unit were adopted throughout the 1990s. At this time the rendering of high resolution VGA standard images could take many hours.[ citation needed ] Fractal generation algorithms display extreme parallelizability. Fractal-generating software was rewritten to make use of multi-threaded processing. Subsequently, the adoption of graphics processing units in computers has greatly increased the speed of rendering and allowed for real-time changes to parameters that were previously impossible due to render delay. [15] 3D fractal generation emerged around 2009. An early list of fractal-generating software was compiled for the book titled Fractals: The Patterns of Chaos by John Briggs published in 1992. [16] Leading writers in the field include Dietmar Saupe, Heinz-Otto Peitgen and Clifford A. Pickover.

Methods

Various trees rendered with an L-system Dragon trees.jpg
Various trees rendered with an L-system

There are two major methods of two dimensional fractal generation. One is to apply an iterative process to simple equations by generative recursion. [6] Dynamical systems produce a series of values. In fractal software values for a set of points on the complex plane are calculated and then rendered as pixels. This computer-based generation of fractal objects is an endless process. In theory, images can be calculated infinitely but in practice are approximated to a certain level of detail. [17] Mandelbrot used quadratic formulas described by the French mathematician Gaston Julia. [14] The maximum fractal dimension that can be produced varies according to type and is sometimes limited according to the method implemented. There are numerous coloring methods that can be applied. One of earliest was the escape time algorithm. [14] Colour banding may appear in images depending on the method of coloring used as well as gradient color density.

Some programs generate geometric self-similar or deterministic fractals such as the Koch curve. These programs use an initiator followed by a generator that is repeated in a pattern. These simple fractals originate from a technique first proposed in 1904 by Koch. [18]

The other main method is with Iterated Function Systems consisting of a number of affine transformations. [19] In the first method each pixel in a fractal image is evaluated according to a function and then coloured, before the same process is applied to the next pixel. The former method represents the classical stochastic approach while the latter implements a linear fractal model. [3] Using recursion allowed programmers to create complex images through simple direction. [20]

Three dimensional fractals are generated in a variety of ways including by using quaternion algebra. [21] Fractals emerge from fluid dynamics modelling simulations as turbulence when contour advection is used to study chaotic mixing.[ citation needed ] The Buddhabrot method was introduced in 1993. Programs might use fractal heightmaps to generate terrain. Fractals have been generated on computers using the following methods: Menger sponge, Hypercomplex manifold, Brownian tree, Brownian motion, Decomposition, L-systems, Lyapunov fractals, Newton fractals, Pickover stalks and Strange attractors.

Features

An animation being created in Chaotica An animation being created in Chaotica.jpg
An animation being created in Chaotica
Fractal created using GIMP Rfl-mandel004-screenshot-03-ls.5.png
Fractal created using GIMP
Simulated landscape using multiple programs Mandelriver.jpg
Simulated landscape using multiple programs

Many different features are included in fractal-generating software packages. A corresponding diversity in the images produced is therefore possible. Most feature some form of algorithm selection, an interactive image zoom, and the ability to save files in JPEG, TIFF, or PNG format, as well as the ability to save parameter files, allowing the user to easily return to previously created images for later modification or exploration. The formula, parameters, variables and coloring algorithms for fractal images can be exchanged between users of the same program. There is no universally adopted standard fractal file format.

One feature of most escape time fractal programs or algebraic-based fractals is a maximum iteration setting. Increasing the iteration count is required if the image is magnified so that fine detail is not lost. Limiting the maximum iterations is important when a device's processing power is low. Coloring options often allow colors to be randomised. Options for color density are common because some gradients output hugely variable magnitudes resulting in heavy repetitive banding or large areas of the same color. Because of the convenient ability to add post-processing effects layering and alpha compositing features found in other graphics software have been included. Both 2D and 3D rendering effects such as plasma effect and lighting may be included. Many packages also allow the user to input their own formula, to allow for greater control of the fractals, as well as a choice of color rendering, along with the use of filters and other image manipulation techniques. Some fractal software packages allow for the creation of movies from a sequence of fractal images. Others display render time and allow some form of color cycling and color palette creation tools.

External media
Images
Searchtool.svg Cover of Scientific American, August 1985
Video
Nuvola apps kaboodle.svg Vol Libre 1980 by Loren Carpenter
Nuvola apps kaboodle.svg Realtime escape-time fractal rendering with a GPU
Nuvola apps kaboodle.svg Four-dimensional raytraced animation in POV-Ray

Standard graphics software (such as GIMP) contains filters or plug-ins which can be used for fractal generation. Blender contains a fractal (or random) modifier. Many stand-alone fractal-generating programs can be used in conjunction with other graphics programs (such as Photoshop) to create more complex images. POV-Ray is a ray tracing program which generates images from a text-based scene description that can generate fractals. Scripts on 3ds Max and Autodesk Maya can be used. A number of web-based interfaces for the fractal generation are freely available including Turtle Graphics Renderer. [22] Fractal Lab can generate both 2D and 3D fractals and is available over the web using WebGL. [23] JWildfire is a java-based, open-source fractal flame generator. [24] Mandelbrot Fractal is a fractal explorer written in JavaScript. [25] Fractal Grower is software written in Java for generating Lindenmayer Substitution Fractals (L-systems). [26]

Programs

Fractal zoom animation on a Julia set Fractals-julia.gif
Fractal zoom animation on a Julia set

Because of the butterfly effect, generating fractals can be difficult to master. A small change in a single variable can have an unpredictable effect. Some software presents the user with a steep learning curve and an understanding of chaos theory is advantageous. This includes the characteristics of fractal dimension, recursion and self-similarity exhibited by all fractals.

Example for an open source program: mandelbulber Mandelbulber v2.24.0 FGS 20210411 20 25 45.png
Example for an open source program: mandelbulber

There are many fractal generating programs available, both free and commercial. Notable fractal generating programs include:

Most of the above programs make two-dimensional fractals, with a few creating three-dimensional fractal objects, such as mandelbulbs and mandelboxes. Mandelbulber is an experimental, cross platform open-source program that generates three-dimensional fractal images. [27] Mandelbulber is adept at producing 3D animations. [28] Mandelbulb 3D is free software for creating 3D images featuring many effects found in 3D rendering environments. [29] Incendia is a 3D fractal program that uses Iterated Function Systems (IFS) for fractal generation. [30] Visions of Chaos, Boxplorer and Fragmentarium also render 3D images.

The open source GnoFract 4D is available. [31] ChaosPro is freeware fractal creation program. [32] Fraqtive is an open source cross platform fractal generator. [33] MandelX is a free program for rendering fractal images on Windows. [34] WinCIG, Chaoscope, Tierazon, Fractal Forge and Malsys also generate fractal images.

See also

Related Research Articles

<span class="mw-page-title-main">Rendering (computer graphics)</span> Process of generating an image from a model

Rendering or image synthesis is the process of generating a photorealistic or non-photorealistic image from a 2D or 3D model by means of a computer program. The resulting image is referred to as the render. Multiple models can be defined in a scene file containing objects in a strictly defined language or data structure. The scene file contains geometry, viewpoint, textures, lighting, and shading information describing the virtual scene. The data contained in the scene file is then passed to a rendering program to be processed and output to a digital image or raster graphics image file. The term "rendering" is analogous to the concept of an artist's impression of a scene. The term "rendering" is also used to describe the process of calculating effects in a video editing program to produce the final video output.

<span class="mw-page-title-main">Fractal</span> Infinitely detailed mathematical structure

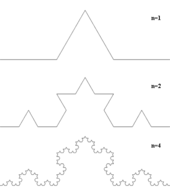
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

<span class="mw-page-title-main">Mandelbrot set</span> Fractal named after mathematician Benoit Mandelbrot

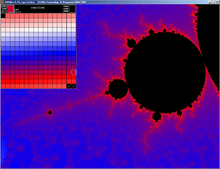
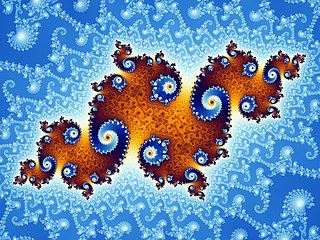
The Mandelbrot set is a two-dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as the complex numbers for which the function does not diverge to infinity when iterated starting at , i.e., for which the sequence , , etc., remains bounded in absolute value.

<span class="mw-page-title-main">Fractal art</span> Form of algorithmic art

Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still digital images, animations, and media. Fractal art developed from the mid-1980s onwards. It is a genre of computer art and digital art which are part of new media art. The mathematical beauty of fractals lies at the intersection of generative art and computer art. They combine to produce a type of abstract art.

<span class="mw-page-title-main">Digital art</span> Collective term for art that is generated digitally with a computer

Digital art refers to any artistic work or practice that uses digital technology as part of the creative or presentation process. It can also refer to computational art that uses and engages with digital media.

Autodesk 3ds Max, formerly 3D Studio and 3D Studio Max, is a professional 3D computer graphics program for making 3D animations, models, games and images. It is developed and produced by Autodesk Media and Entertainment. It has modeling capabilities and a flexible plugin architecture and must be used on the Microsoft Windows platform. It is frequently used by video game developers, many TV commercial studios, and architectural visualization studios. It is also used for movie effects and movie pre-visualization. 3ds Max features shaders, dynamic simulation, particle systems, radiosity, normal map creation and rendering, global illumination, a customizable user interface, and its own scripting language.

<span class="mw-page-title-main">Buddhabrot</span> Probability distribution over the trajectories of points that escape the Mandelbrot fractal

The Buddhabrot is the probability distribution over the trajectories of points that escape the Mandelbrot fractal. Its name reflects its pareidolic resemblance to classical depictions of Gautama Buddha, seated in a meditation pose with a forehead mark (tikka), a traditional oval crown (ushnisha), and ringlet of hair.

<span class="mw-page-title-main">Real-time computer graphics</span> Sub-field of computer graphics

Real-time computer graphics or real-time rendering is the sub-field of computer graphics focused on producing and analyzing images in real time. The term can refer to anything from rendering an application's graphical user interface (GUI) to real-time image analysis, but is most often used in reference to interactive 3D computer graphics, typically using a graphics processing unit (GPU). One example of this concept is a video game that rapidly renders changing 3D environments to produce an illusion of motion.

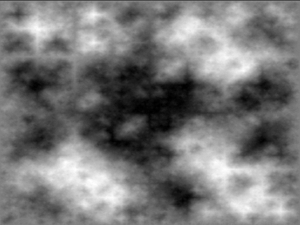
<span class="mw-page-title-main">Diamond-square algorithm</span> Method for generating heightmaps for computer graphics

The diamond-square algorithm is a method for generating heightmaps for computer graphics. It is a slightly better algorithm than the three-dimensional implementation of the midpoint displacement algorithm, which produces two-dimensional landscapes. It is also known as the random midpoint displacement fractal, the cloud fractal or the plasma fractal, because of the plasma effect produced when applied.

<span class="mw-page-title-main">Hilbert curve</span> Space-filling curve

The Hilbert curve is a continuous fractal space-filling curve first described by the German mathematician David Hilbert in 1891, as a variant of the space-filling Peano curves discovered by Giuseppe Peano in 1890.

<span class="mw-page-title-main">Burning Ship fractal</span> Complex plane fractal

The Burning Ship fractal, first described and created by Michael Michelitsch and Otto E. Rössler in 1992, is generated by iterating the function:

VistaPro is 3D scenery generator for the Amiga, Macintosh, MS-DOS, and Microsoft Windows. It was written by John Hinkley as the follow-up to the initial version, Vista. The about box describes it as "a 3-D landscape generator and projector capable of accurately displaying real-world and fractal landscapes." It was published by Virtual Reality Labs and developed by Hypercube Engineering. The latest versions were published and developed by Monkey Byte Development.

<span class="mw-page-title-main">3D computer graphics</span> Graphics that use a three-dimensional representation of geometric data

3D computer graphics, sometimes called CGI, 3-D-CGI or three-dimensional computer graphics, are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering digital images, usually 2D images but sometimes 3D images. The resulting images may be stored for viewing later or displayed in real time.

<span class="mw-page-title-main">Scenery generator</span> Type of software

A scenery generator is software used to create landscape images, 3D models, and animations. These programs often use procedural generation to generate the landscapes. If not using procedural generation to create the landscapes, then normally a 3D artist would render and create the landscapes. These programs are often used in video games or movies. Basic elements of landscapes created by scenery generators include terrain, water, foliage, and clouds. The process for basic random generation uses a diamond square algorithm.

<span class="mw-page-title-main">Mandelbulb</span> Three-dimensional fractal

The Mandelbulb is a three-dimensional fractal, constructed for the first time in 1997 by Jules Ruis and in 2009 further developed by Daniel White and Paul Nylander using spherical coordinates.

<span class="mw-page-title-main">Orbit trap</span> Method of colouring fractal images

In mathematics, an orbit trap is a method of colouring fractal images based upon how close an iterative function, used to create the fractal, approaches a geometric shape, called a "trap". Typical traps are points, lines, circles, flower shapes and even raster images. Orbit traps are typically used to colour two dimensional fractals representing the complex plane.

<span class="mw-page-title-main">Ultra Fractal</span>

Ultra Fractal is a fractal generation and rendering software application. The program was the first publicly available fractal software which featured layering methods previously only found in image editing software. Because of this, the program has become popular for use in the creation of fractal art.

<span class="mw-page-title-main">Computer-generated imagery</span> Application of computer graphics to create or contribute to images

Computer-generated imagery (CGI) is a specific-technology or application of computer graphics for creating or improving images in art, printed media, simulators, videos and video games. These images are either static or dynamic. CGI both refers to 2D computer graphics and 3D computer graphics with the purpose of designing characters, virtual worlds, or scenes and special effects. The application of CGI for creating/improving animations is called computer animation, or CGI animation.

This is a glossary of terms relating to computer graphics.

References

  1. ↑ Frame, Michael; Amelia Urry (2016). Fractal Worlds: Grown, Built, and Imagined. Yale University Press. p. 129. ISBN   978-0300197877 . Retrieved 5 May 2017.
  2. ↑ F. v., Haeseler v.; H.-O Peitgen; G. Skordev (2012). "Linear Cellular Automata, Substitutions, Hierarchical Iterated Function Systems and Attractors". In Encarnacao, Jose L.; Peitgen, Heinz-Otto; Sakas, Georgios; Englert, Gabriele (eds.). Fractal Geometry and Computer Graphics. Springer Science & Business Media. p. 3. ISBN   9783642956782 . Retrieved 7 May 2017.
  3. 1 2 Nikiel¹, Slawomir S (October 1998). "True-colour images and iterated function systems". Computers & Graphics. 22 (5): 635–640. doi:10.1016/S0097-8493(98)00072-7.
  4. ↑ Janus Kopfstein (14 May 2014). "This 4-kilobyte demo squeezes a universe of fractals into the size of a Word document". The Verge. Vox Media. Retrieved 5 March 2017.
  5. ↑ Malyshkin, Victor (2013). Parallel Computing Technologies: 12th International Conference, PaCT 2013, St. Petersburg, Russia, September 30-October 4, 2013, Proceedings. Springer. p. 267. ISBN   9783642399589 . Retrieved 7 May 2017.
  6. 1 2 Daniel Shiffman. "Chapter 8. Fractals". The Nature of Code. Retrieved 22 Jan 2024.
  7. ↑ Gleick, James (1987). Chaos: Making a New Science. Cardinal. pp. 222–223. ISBN   978-0143113454.
  8. ↑ Tom Van Cutsem. "Session 5 - Escape-Time Fractals" . Retrieved 7 March 2017.
  9. ↑ Röss, Dieter (2011). Learning and Teaching Mathematics using Simulations: Plus 2000 Examples from Physics. Walter de Gruyter. p. 56. ISBN   9783110250077 . Retrieved 7 May 2017.
  10. ↑ "Vol Libre: The First Fractal CGI Movie". History of Information. Jeremy Norman & Co. Retrieved 5 March 2017.
  11. ↑ "Susan Stepney Professor of Computer Science, University of York, UK". www-users.cs.york.ac.uk. University of York. Retrieved 29 December 2018.
  12. ↑ Stepney, Susan (October 1983). "Incredible fractals, pp 37, 39, 41 and 43". www-users.cs.york.ac.uk. AcornUser. Retrieved 29 December 2018.
  13. ↑ Stepney, Susan (March 1984). "Snowflakes and other monsters, pp 25, 28, 29". www-users.cs.york.ac.uk. AcornUser. Retrieved 29 December 2018.
  14. 1 2 3 Garcia, Francisco; Fernandez, Angel; Barrallo, Javier; Martin, Luis. "Coloring dynamical systems in the complex plane". CiteSeerX   10.1.1.393.9370 .
  15. ↑ W.D. Mayfield; J.C. Eilan; T.J. Hu; M.C. Paulsen; B.M. Wyatt (2016). "Fractal Art Generation using GPUs". arXiv: 1611.03079 [cs.GR].
  16. ↑ Briggs, John (1992). Fractals: The Patterns of Chaos . Simon and Schuster. p.  182. ISBN   978-0671742171.
  17. ↑ Chen, J-N; N M Thalmann; Z-S Tsang; D Thalmann (1994). Fundamentals of Computer Graphics. World Scientific. p. 100. ISBN   9789814603744 . Retrieved 5 May 2017.
  18. ↑ Russ, John C. (2013). Fractal Surfaces. Springer Science & Business Media. p. 150. ISBN   978-1489925787 . Retrieved 5 May 2017.
  19. ↑ Chen’, Yan Qiu; Bi, Guoan (May–June 1997). "3-D IFS fractals as real-time graphics model". Computers & Graphics. 21 (3): 367–370. doi:10.1016/S0097-8493(97)00014-9.
  20. ↑ Peitgen, Heinz-Otto; Peter Richter (1986). The Beauty of Fractals. Springer-Verlag. p. 2. ISBN   978-0883859711 . Retrieved 7 May 2017.
  21. ↑ Leys, Jos (June 2005). "Sphere inversion fractals". Computers & Graphics. 29 (3): 463–466. doi:10.1016/j.cag.2005.03.011.
  22. ↑ "Turtle Graphics Renderer" . Retrieved 2 March 2017.
  23. ↑ "Fractal Lab". subblue.com. Retrieved 5 March 2017.
  24. ↑ "Welcome to the official home of the JWildfire software!" . Retrieved 7 March 2017.
  25. ↑ Mike Williams (17 July 2016). "Mandelbrot Fractal". PCAdvisor. IDG UK. Retrieved 5 March 2017.
  26. ↑ "Fractal Grower". The University of New Mexico. Retrieved 6 March 2017.
  27. ↑ Joey Bernard (7 January 2014). "Taking Fractals off the Page". Linux Journal. Retrieved 5 May 2017.
  28. ↑ Mike Williams (25 November 2013). "Generate spectacular 3D fractals with Mandelbulber". BetaNews. Retrieved 5 March 2017.
  29. ↑ "Mandelbulb 3D (MB3D) Fractal Rendering Software". SphereLab. 17 January 2014. Retrieved 7 March 2017.
  30. ↑ "Incendia". Ramiro Pérez Clare Nash. Retrieved 7 March 2017.
  31. ↑ "Gnofract 4D". Archived from the original on 6 March 2020. Retrieved 2 March 2017.
  32. ↑ "ChaosPro Release 4.0" . Retrieved 2 March 2017.
  33. ↑ "Fraqtive" . Retrieved 2 March 2017.
  34. ↑ "Free software from Falcosoft". Falcosoft. 27 January 2017. Retrieved 5 March 2017.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.