List of map projections

This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources.

This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise notable. Because there is no limit to the number of possible map projections, ^[1] there can be no comprehensive list.

Table of projections

Year	Projection	Image	Type	Properties	Creator	Notes
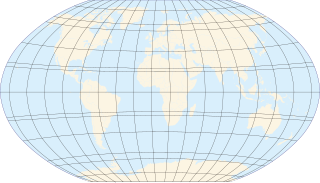
0120 c. 120	Equirectangular = equidistant cylindrical = rectangular = la carte parallélogrammatique		Cylindrical	Equidistant	Marinus of Tyre	Simplest geometry; distances along meridians are conserved. Plate carrée: special case having the equator as the standard parallel.
1745	Cassini = Cassini–Soldner		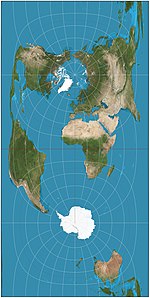Cylindrical	Equidistant	César-François Cassini de Thury	Transverse of equirectangular projection; distances along central meridian are conserved. Distances perpendicular to central meridian are preserved.
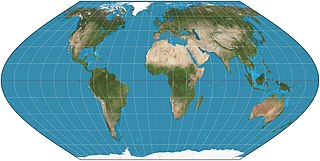
1569	Mercator = Wright		Cylindrical	Conformal	Gerardus Mercator	Lines of constant bearing (rhumb lines) are straight, aiding navigation. Areas inflate with latitude, becoming so extreme that the map cannot show the poles.
2005	Web Mercator		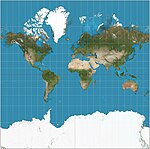Cylindrical	Compromise	Google	Variant of Mercator that ignores Earth's ellipticity for fast calculation, and clips latitudes to ~85.05° for square presentation. De facto standard for Web mapping applications.
1822	Gauss–Krüger = Gauss conformal = (ellipsoidal) transverse Mercator		Cylindrical	Conformal	Carl Friedrich Gauss Johann Heinrich Louis Krüger	This transverse, ellipsoidal form of the Mercator is finite, unlike the equatorial Mercator. Forms the basis of the Universal Transverse Mercator coordinate system.
1922	Roussilhe oblique stereographic				Henri Roussilhe
1903	Hotine oblique Mercator		Cylindrical	Conformal	M. Rosenmund, J. Laborde, Martin Hotine
1855	Gall stereographic		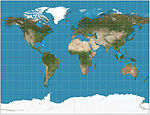Cylindrical	Compromise	James Gall	Intended to resemble the Mercator while also displaying the poles. Standard parallels at 45°N/S.
1942	Miller = Miller cylindrical		Cylindrical	Compromise	Osborn Maitland Miller	Intended to resemble the Mercator while also displaying the poles.
1772	Lambert cylindrical equal-area		Cylindrical	Equal-area	Johann Heinrich Lambert	Cylindrical equal-area projection with standard parallel at the equator and an aspect ratio of π (3.14).
1910	Behrmann		Cylindrical	Equal-area	Walter Behrmann	Cylindrical equal-area projection with standard parallels at 30°N/S and an aspect ratio of (3/4)π ≈ 2.356.
2002	Hobo–Dyer		Cylindrical	Equal-area	Mick Dyer	Cylindrical equal-area projection with standard parallels at 37.5°N/S and an aspect ratio of 1.977. Similar are Trystan Edwards with standard parallels at 37.4° and Smyth equal surface (=Craster rectangular) with standard parallels around 37.07°.
1855	Gall–Peters = Gall orthographic = Peters		Cylindrical	Equal-area	James Gall (Arno Peters)	Cylindrical equal-area projection with standard parallels at 45°N/S and an aspect ratio of π/2 ≈ 1.571. Similar is Balthasart with standard parallels at 50°N/S and Tobler’s world in a square with standard parallels around 55.66°N/S.
1850 c. 1850	Central cylindrical		Cylindrical	Perspective	(unknown)	Practically unused in cartography because of severe polar distortion, but popular in panoramic photography, especially for architectural scenes.
1600 c. 1600	Sinusoidal = Sanson–Flamsteed = Mercator equal-area		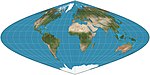Pseudocylindrical	Equal-area, equidistant	(Several; first is unknown)	Meridians are sinusoids; parallels are equally spaced. Aspect ratio of 2:1. Distances along parallels are conserved.
1805	Mollweide = elliptical = Babinet = homolographic		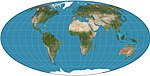Pseudocylindrical	Equal-area	Karl Brandan Mollweide	Meridians are ellipses.
1953	Sinu-Mollweide		Pseudocylindrical	Equal-area	Allen K. Philbrick	A combination of the last two projections, hence its name.
1906	Eckert II		Pseudocylindrical	Equal-area	Max Eckert-Greifendorff
1906	Eckert IV		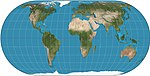Pseudocylindrical	Equal-area	Max Eckert-Greifendorff	Parallels are unequal in spacing and scale; outer meridians are semicircles; other meridians are semiellipses.
1906	Eckert VI		Pseudocylindrical	Equal-area	Max Eckert-Greifendorff	Parallels are unequal in spacing and scale; meridians are half-period sinusoids.
1540	Ortelius oval		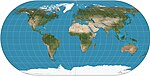Pseudocylindrical	Compromise	Battista Agnese	Meridians are circular. [2]
1923	Goode homolosine		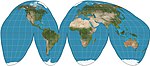Pseudocylindrical	Equal-area	John Paul Goode	Hybrid of Sinusoidal and Mollweide projections. Usually used in interrupted form.
1939	Kavrayskiy VII		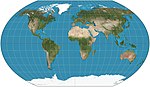Pseudocylindrical	Compromise	Vladimir V. Kavrayskiy	Evenly spaced parallels. Equivalent to Wagner VI horizontally compressed by a factor of ${\displaystyle {\sqrt {3}}/{2}}$.
1963	Robinson		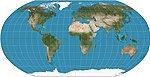Pseudocylindrical	Compromise	Arthur H. Robinson	Computed by interpolation of tabulated values. Used by Rand McNally since inception and used by NGS in 1988–1998.
2018	Equal Earth		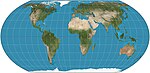Pseudocylindrical	Equal-area	Bojan Šavrič, Tom Patterson, Bernhard Jenny	Inspired by the Robinson projection, but retains the relative size of areas.
2011	Natural Earth		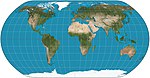Pseudocylindrical	Compromise	Tom Patterson	Originally by interpolation of tabulated values. Now has a polynomial.
1973	Tobler hyperelliptical		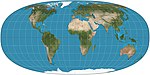Pseudocylindrical	Equal-area	Waldo R. Tobler	A family of map projections that includes as special cases Mollweide projection, Collignon projection, and the various cylindrical equal-area projections.
1932	Wagner VI		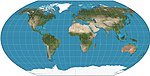Pseudocylindrical	Compromise	K. H. Wagner	Equivalent to Kavrayskiy VII vertically compressed by a factor of ${\displaystyle {\sqrt {3}}/{2}}$.
1865 c. 1865	Collignon		Pseudocylindrical	Equal-area	Édouard Collignon	Depending on configuration, the projection also may map the sphere to a single diamond or a pair of squares.
1997	HEALPix		Pseudocylindrical	Equal-area	Krzysztof M. Górski	Hybrid of Collignon + Lambert cylindrical equal-area.
1929	Boggs eumorphic		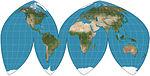Pseudocylindrical	Equal-area	Samuel Whittemore Boggs	The equal-area projection that results from average of sinusoidal and Mollweide y-coordinates and thereby constraining the x coordinate.
1929	Craster parabolic =Putniņš P4		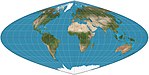Pseudocylindrical	Equal-area	John Craster	Meridians are parabolas. Standard parallels at 36°46′N/S; parallels are unequal in spacing and scale; 2:1 aspect.
1949	McBryde–Thomas flat-pole quartic = McBryde–Thomas #4		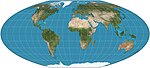Pseudocylindrical	Equal-area	Felix W. McBryde, Paul Thomas	Standard parallels at 33°45′N/S; parallels are unequal in spacing and scale; meridians are fourth-order curves. Distortion-free only where the standard parallels intersect the central meridian.
1937 1944	Quartic authalic		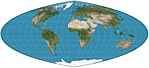Pseudocylindrical	Equal-area	Karl Siemon Oscar Adams	Parallels are unequal in spacing and scale. No distortion along the equator. Meridians are fourth-order curves.
1965	The Times		Pseudocylindrical	Compromise	John Muir	Standard parallels 45°N/S. Parallels based on Gall stereographic, but with curved meridians. Developed for Bartholomew Ltd., The Times Atlas.
1935 1966	Loximuthal		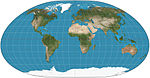Pseudocylindrical	Compromise	Karl Siemon Waldo R. Tobler	From the designated centre, lines of constant bearing (rhumb lines/loxodromes) are straight and have the correct length. Generally asymmetric about the equator.
1889	Aitoff		Pseudoazimuthal	Compromise	David A. Aitoff	Stretching of modified equatorial azimuthal equidistant map. Boundary is 2:1 ellipse. Largely superseded by Hammer.
1892	Hammer = Hammer–Aitoff variations: Briesemeister; Nordic		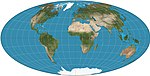Pseudoazimuthal	Equal-area	Ernst Hammer	Modified from azimuthal equal-area equatorial map. Boundary is 2:1 ellipse. Variants are oblique versions, centred on 45°N.
1994	Strebe 1995		Pseudoazimuthal	Equal-area	Daniel "daan" Strebe	Formulated by using other equal-area map projections as transformations.
1921	Winkel tripel		Pseudoazimuthal	Compromise	Oswald Winkel	Arithmetic mean of the equirectangular projection and the Aitoff projection. Standard world projection for the NGS since 1998.
1904	Van der Grinten		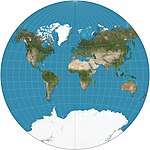Other	Compromise	Alphons J. van der Grinten	Boundary is a circle. All parallels and meridians are circular arcs. Usually clipped near 80°N/S. Standard world projection of the NGS in 1922–1988.
0150 c. 150	Equidistant conic = simple conic		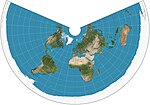Conic	Equidistant	Based on Ptolemy's 1st Projection	Distances along meridians are conserved, as is distance along one or two standard parallels. [3]
1772	Lambert conformal conic		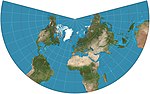Conic	Conformal	Johann Heinrich Lambert	Used in aviation charts.
1805	Albers conic		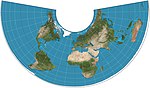Conic	Equal-area	Heinrich C. Albers	Two standard parallels with low distortion between them.
1500 c. 1500	Werner		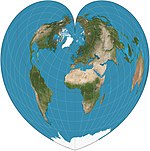Pseudoconical	Equal-area, equidistant	Johannes Stabius	Parallels are equally spaced concentric circular arcs. Distances from the North Pole are correct as are the curved distances along parallels and distances along central meridian.
1511	Bonne		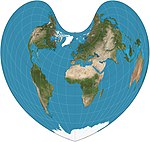Pseudoconical, cordiform	Equal-area, equidistant	Bernardus Sylvanus	Parallels are equally spaced concentric circular arcs and standard lines. Appearance depends on reference parallel. General case of both Werner and sinusoidal.
2003	Bottomley		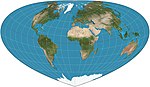Pseudoconical	Equal-area	Henry Bottomley	Alternative to the Bonne projection with simpler overall shape Parallels are elliptical arcs Appearance depends on reference parallel.
1820 c. 1820	American polyconic		Pseudoconical	Compromise	Ferdinand Rudolph Hassler	Distances along the parallels are preserved as are distances along the central meridian.
1853 c. 1853	Rectangular polyconic		Pseudoconical	Compromise	United States Coast Survey	Latitude along which scale is correct can be chosen. Parallels meet meridians at right angles.
1963	Latitudinally equal-differential polyconic		Pseudoconical	Compromise	China State Bureau of Surveying and Mapping	Polyconic: parallels are non-concentric arcs of circles.
1000 c. 1000	Nicolosi globular		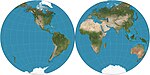Pseudoconical [4]	Compromise	Abū Rayḥān al-Bīrūnī; reinvented by Giovanni Battista Nicolosi, 1660. [1] : 14
1000 c. 1000	Azimuthal equidistant =Postel =zenithal equidistant		Azimuthal	Equidistant	Abū Rayḥān al-Bīrūnī	Distances from center are conserved. Used as the emblem of the United Nations, extending to 60° S.
c. 580 BC	Gnomonic		Azimuthal	Gnomonic	Thales (possibly)	All great circles map to straight lines. Extreme distortion far from the center. Shows less than one hemisphere.
1772	Lambert azimuthal equal-area		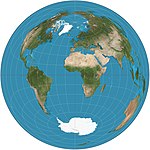Azimuthal	Equal-area	Johann Heinrich Lambert	The straight-line distance between the central point on the map to any other point is the same as the straight-line 3D distance through the globe between the two points.
c. 200 BC	Stereographic		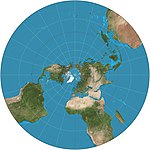Azimuthal	Conformal	Hipparchos*	Map is infinite in extent with outer hemisphere inflating severely, so it is often used as two hemispheres. Maps all small circles to circles, which is useful for planetary mapping to preserve the shapes of craters.
c. 200 BC	Orthographic		Azimuthal	Perspective	Hipparchos*	View from an infinite distance.
1740	Vertical perspective		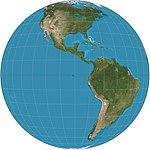Azimuthal	Perspective	Matthias Seutter*	View from a finite distance. Can only display less than a hemisphere.
1919	Two-point equidistant		Azimuthal	Equidistant	Hans Maurer	Two "control points" can be almost arbitrarily chosen. The two straight-line distances from any point on the map to the two control points are correct.
2021	Gott, Goldberg and Vanderbei’s		Azimuthal	Equidistant	J. Richard Gott, Goldberg and Robert J. Vanderbei	Gott, Goldberg and Vanderbei’s double-sided disk map was designed to minimize all six types of map distortions. Not properly "a" map projection because it is on two surfaces instead of one, it consists of two hemispheric equidistant azimuthal projections back-to-back. [5] [6] [7]
1879	Peirce quincuncial		Other	Conformal	Charles Sanders Peirce	Tessellates. Can be tiled continuously on a plane, with edge-crossings matching except for four singular points per tile.
1887	Guyou hemisphere-in-a-square projection		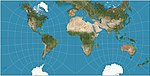Other	Conformal	Émile Guyou	Tessellates.
1925	Adams hemisphere-in-a-square projection		Other	Conformal	Oscar Sherman Adams
1965	Lee conformal world on a tetrahedron		Polyhedral	Conformal	L. P. Lee	Projects the globe onto a regular tetrahedron. Tessellates.
1514	Octant projection		Polyhedral	Compromise	Leonardo da Vinci	Projects the globe onto eight octants (Reuleaux triangles) with no meridians and no parallels.
1909	Cahill's butterfly map		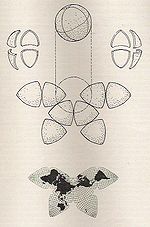Polyhedral	Compromise	Bernard Joseph Stanislaus Cahill	Projects the globe onto an octahedron with symmetrical components and contiguous landmasses that may be displayed in various arrangements.
1975	Cahill–Keyes projection		Polyhedral	Compromise	Gene Keyes	Projects the globe onto a truncated octahedron with symmetrical components and contiguous land masses that may be displayed in various arrangements.
1996	Waterman butterfly projection		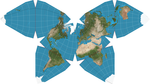Polyhedral	Compromise	Steve Waterman	Projects the globe onto a truncated octahedron with symmetrical components and contiguous land masses that may be displayed in various arrangements.
1973	Quadrilateralized spherical cube		Polyhedral	Equal-area	F. Kenneth Chan, E. M. O'Neill
1943	Dymaxion map		Polyhedral	Compromise	Buckminster Fuller	Also known as a Fuller Projection.
1999	AuthaGraph projection		Polyhedral	Compromise	Hajime Narukawa	Approximately equal-area. Tessellates.
2008	Myriahedral projections		Polyhedral	Equal-area	Jarke J. van Wijk	Projects the globe onto a myriahedron: a polyhedron with a very large number of faces. [8] [9]
1909	Craig retroazimuthal = Mecca		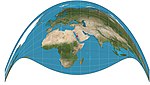Retroazimuthal	Compromise	James Ireland Craig
1910	Hammer retroazimuthal, front hemisphere		Retroazimuthal		Ernst Hammer
1910	Hammer retroazimuthal, back hemisphere		Retroazimuthal		Ernst Hammer
1833	Littrow		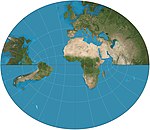Retroazimuthal	Conformal	Joseph Johann Littrow	on equatorial aspect it shows a hemisphere except for poles.
1943	Armadillo		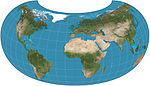Other	Compromise	Erwin Raisz
1982	GS50		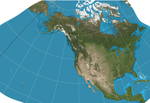Other	Conformal	John P. Snyder	Designed specifically to minimize distortion when used to display all 50 U.S. states.
1941	Wagner VII = Hammer-Wagner		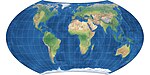Pseudoazimuthal	Equal-area	K. H. Wagner
1947?	Chamberlin trimetric projection		Other	Compromise	Wellman Chamberlin	Many National Geographic Society maps of single continents use this projection.
1948	Atlantis = Transverse Mollweide		Pseudocylindrical	Equal-area	John Bartholomew	Oblique version of Mollweide
1953	Bertin = Bertin-Rivière = Bertin 1953		Other	Compromise	Jacques Bertin	Projection in which the compromise is no longer homogeneous but instead is modified for a larger deformation of the oceans, to achieve lesser deformation of the continents. Commonly used for French geopolitical maps. [10]
2002	Hao projection		Pseudoconical	Compromise	Hao Xiaoguang	Known as "plane terrestrial globe", [11] it was adopted by the People's Liberation Army for the official military maps and China’s State Oceanic Administration for polar expeditions. [12] [13]

*The first known popularizer/user and not necessarily the creator.

Key

Main article: Map projection

Type of projection surface

Cylindrical

In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines.

Pseudocylindrical

In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels.

Conic

In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles.

Pseudoconical

In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as circular arcs.

Azimuthal

In standard presentation, azimuthal projections map meridians as straight lines and parallels as complete, concentric circles. They are radially symmetrical. In any presentation (or aspect), they preserve directions from the center point. This means great circles through the central point are represented by straight lines on the map.

Pseudoazimuthal

In normal aspect, pseudoazimuthal projections map the equator and central meridian to perpendicular, intersecting straight lines. They map parallels to complex curves bowing away from the equator, and meridians to complex curves bowing in toward the central meridian. Listed here after pseudocylindrical as generally similar to them in shape and purpose.

Other

Typically calculated from formula, and not based on a particular projection

Polyhedral maps

Polyhedral maps can be folded up into a polyhedral approximation to the sphere, using particular projection to map each face with low distortion.

Properties

Conformal

Preserves angles locally, implying that local shapes are not distorted and that local scale is constant in all directions from any chosen point.

Equal-area

Area measure is conserved everywhere.

Compromise

Neither conformal nor equal-area, but a balance intended to reduce overall distortion.

Equidistant

All distances from one (or two) points are correct. Other equidistant properties are mentioned in the notes.

Gnomonic

All great circles are straight lines.

Retroazimuthal

Direction to a fixed location B (by the shortest route) corresponds to the direction on the map from A to B.

Perspective

Can be constructed by light shining through a globe onto a developable surface.

See also

• 360 video projection
• List of national coordinate reference systems
• Snake Projection

Notes

1. Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections. University of Chicago Press. p. 1. ISBN   0-226-76746-9.
2. Donald Fenna (2006). Cartographic Science: A Compendium of Map Projections, with Derivations. CRC Press. p. 249. ISBN   978-0-8493-8169-0.
3. Furuti, Carlos A. "Conic Projections: Equidistant Conic Projections". Archived from the original on November 30, 2012. Retrieved February 11, 2020.
4. ""Nicolosi Globular projection"" (PDF). Archived (PDF) from the original on 2016-04-29. Retrieved 2016-09-18.
5. "New Earth Map Projection". vanderbei.princeton.edu. Retrieved 2023-04-27.
6. Fuller-Wright, Liz. "Princeton astrophysicists re-imagine world map, designing a less distorted, 'radically different' way to see the world". Princeton University. Archived from the original on 2022-07-13. Retrieved 2022-07-13.
7. Gott III, J. Richard; Goldberg, David M.; Vanderbei, Robert J. (2021-02-15). "Flat Maps that improve on the Winkel Tripel". arXiv: 2102.08176 [astro-ph.IM].
8. Jarke J. van Wijk. "Unfolding the Earth: Myriahedral Projections". Archived from the original on 2020-06-20. Retrieved 2011-03-08.
9. Carlos A. Furuti. "Interrupted Maps: Myriahedral Maps". Archived from the original on 2020-01-17. Retrieved 2011-11-03.
10. Rivière, Philippe (October 1, 2017). "Bertin Projection (1953)". visionscarto. Archived from the original on January 27, 2020. Retrieved January 27, 2020.
11. Hao, Xiaoguang; Xue, Huaiping. "Generalized Equip-Difference Parallel Polyconical Projection Method for the Global Map" (PDF). Archived (PDF) from the original on February 9, 2023. Retrieved February 14, 2023.
12. Alexeeva, Olga; Lasserre, Frédéric (October 20, 2022). "Le concept de troisième pôle: cartes et représentations polaires de la Chine". Géoconfluences (in French). Archived from the original on February 14, 2023. Retrieved February 14, 2023.
13. Vriesema, Jochem (April 7, 2021). "Arctic geopolitics: China's remapping of the world". Clingendael Spectator. The Hague: Clingendael. Archived from the original on February 14, 2023. Retrieved February 14, 2023.

Further reading

• Snyder, John P. (1987). Map projections – A working manual (PDF). U.S. Geological Survey Professional Paper. Vol. 1395. Washington, D.C.: U.S. Government Printing Office. doi:10.3133/pp1395 . Retrieved 2019-02-18.
• Snyder, John P.; Voxland, Philip M. (1989). An Album of Map Projections (PDF). U.S. Geological Survey Professional Paper. Vol. 1453. Washington, D.C.: U.S. Government Printing Office. doi:10.3133/pp1453 . Retrieved 2019-02-18.