Related Research Articles

Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in nonlinear media, that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity is typically observed only at very high light intensities (when the electric field of the light is >108 V/m and thus comparable to the atomic electric field of ~1011 V/m) such as those provided by lasers. Above the Schwinger limit, the vacuum itself is expected to become nonlinear. In nonlinear optics, the superposition principle no longer holds.
In physics, coherence expresses the potential for two waves to interfere. Two monochromatic beams from a single source always interfere. Physical sources are not strictly monochromatic: they may be partly coherent. Beams from different sources are mutually incoherent.

Martin David Kruskal was an American mathematician and physicist. He made fundamental contributions in many areas of mathematics and science, ranging from plasma physics to general relativity and from nonlinear analysis to asymptotic analysis. His most celebrated contribution was in the theory of solitons.

In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.

Philip John Holmes is the Eugene Higgins Professor of Mechanical and Aerospace Engineering at Princeton University. As a member of the Mechanical and Aerospace Engineering department, he formerly served as the interim chair until May 2007.
In continuum mechanics, wave turbulence is a set of nonlinear waves deviated far from thermal equilibrium. Such a state is usually accompanied by dissipation. It is either decaying turbulence or requires an external source of energy to sustain it. Examples are waves on a fluid surface excited by winds or ships, and waves in plasma excited by electromagnetic waves etc.
Dissipative solitons (DSs) are stable solitary localized structures that arise in nonlinear spatially extended dissipative systems due to mechanisms of self-organization. They can be considered as an extension of the classical soliton concept in conservative systems. An alternative terminology includes autosolitons, spots and pulses.
Mark Jay Ablowitz is a professor in the department of Applied Mathematics at the University of Colorado at Boulder, Colorado. He was born in New York City.

Vladimir Evgen'evich Zakharov is a Soviet and Russian mathematician and physicist. He is currently Regents' Professor of mathematics at The University of Arizona, director of the Mathematical Physics Sector at the Lebedev Physical Institute, and is on the committee of the Stefanos Pnevmatikos International Award. Zakharov's research interests cover physical aspects of nonlinear wave theory in plasmas, hydrodynamics, oceanology, geophysics, solid state physics, optics, and general relativity.
In physical optics or wave optics, a vector soliton is a solitary wave with multiple components coupled together that maintains its shape during propagation. Ordinary solitons maintain their shape but have effectively only one (scalar) polarization component, while vector solitons have two distinct polarization components. Among all the types of solitons, optical vector solitons draw the most attention due to their wide range of applications, particularly in generating ultrafast pulses and light control technology. Optical vector solitons can be classified into temporal vector solitons and spatial vector solitons. During the propagation of both temporal solitons and spatial solitons, despite being in a medium with birefringence, the orthogonal polarizations can copropagate as one unit without splitting due to the strong cross-phase modulation and coherent energy exchange between the two polarizations of the vector soliton which may induce intensity differences between these two polarizations. Thus vector solitons are no longer linearly polarized but rather elliptically polarized.
In the fields of nonlinear optics and fluid dynamics, modulational instability or sideband instability is a phenomenon whereby deviations from a periodic waveform are reinforced by nonlinearity, leading to the generation of spectral-sidebands and the eventual breakup of the waveform into a train of pulses.

Mikhail Izrailevich Rabinovich (MIR) is a Russian influential physicist and neuroscientist working in the field of nonlinear dynamics and its applications. His work helped shape the understanding of dynamical systems.
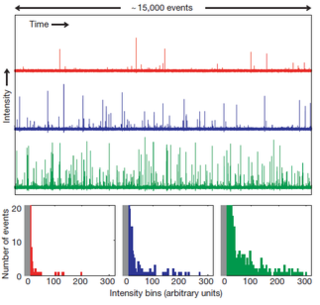
Optical rogue waves are rare pulses of light analogous to rogue or freak ocean waves. The term optical rogue waves was coined to describe rare pulses of broadband light arising during the process of supercontinuum generation—a noise-sensitive nonlinear process in which extremely broadband radiation is generated from a narrowband input waveform—in nonlinear optical fiber. In this context, optical rogue waves are characterized by an anomalous surplus in energy at particular wavelengths or an unexpected peak power. These anomalous events have been shown to follow heavy-tailed statistics, also known as L-shaped statistics, fat-tailed statistics, or extreme-value statistics. These probability distributions are characterized by long tails: large outliers occur rarely, yet much more frequently than expected from Gaussian statistics and intuition. Such distributions also describe the probabilities of freak ocean waves and various phenomena in both the man-made and natural worlds. Despite their infrequency, rare events wield significant influence in many systems. Aside from the statistical similarities, light waves traveling in optical fibers are known to obey the similar mathematics as water waves traveling in the open ocean, supporting the analogy between oceanic rogue waves and their optical counterparts. More generally, research has exposed a number of different analogies between extreme events in optics and hydrodynamic systems. A key practical difference is that most optical experiments can be done with a table-top apparatus, offer a high degree of experimental control, and allow data to be acquired extremely rapidly. Consequently, optical rogue waves are attractive for experimental and theoretical research and have become a highly studied phenomenon. The particulars of the analogy between extreme waves in optics and hydrodynamics may vary depending on the context, but the existence of rare events and extreme statistics in wave-related phenomena are common ground.

In continuum mechanics, an energy cascade involves the transfer of energy from large scales of motion to the small scales or a transfer of energy from the small scales to the large scales. This transfer of energy between different scales requires that the dynamics of the system is nonlinear. Strictly speaking, a cascade requires the energy transfer to be local in scale, evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain.

Luigi Lugiato is an Italian physicist and professor emeritus at University of Insubria (Varese/Como). He is best known for his work in theoretical nonlinear and quantum optics, and especially for the Lugiato–Lefever equation (LLE,). He has authored more than 340 scientific articles, and the textbook Nonlinear Dynamical Systems. His work has been theoretical but has stimulated a large number of important experiments in the world. It is also characterized by the fact of combining the classical and quantum aspects of optical systems.
Kerr frequency combs are optical frequency combs which are generated from a continuous wave pump laser by the Kerr nonlinearity. This coherent conversion of the pump laser to a frequency comb takes place inside an optical resonator which is typically of micrometer to millimeter in size and is therefore termed a microresonator. The coherent generation of the frequency comb from a continuous wave laser with the optical nonlinearity as a gain sets Kerr frequency combs apart from today’s most common optical frequency combs. These frequency combs are generated by mode-locked lasers where the dominating gain stems from a conventional laser gain medium, which is pumped incoherently. Because Kerr frequency combs only rely on the nonlinear properties of the medium inside the microresonator and do not require a broadband laser gain medium, broad Kerr frequency combs can in principle be generated around any pump frequency.
Joceline Claude Lega is a French physicist and applied mathematician, interested in nonlinear dynamics. She is a professor in the departments of mathematics, applied mathematics, and epidemiology and biostatistics at the University of Arizona, and editor-in-chief of Physica D.
The numerical models of lasers and the most of nonlinear optical systems stem from Maxwell–Bloch equations (MBE). This full set of Partial Differential Equations includes Maxwell equations for electromagnetic field and semiclassical equations of the two-level atoms. For this reason the simplified theoretical approaches were developed for numerical simulation of laser beams formation and their propagation since the early years of laser era. The Slowly varying envelope approximation of MBE follows from the standard nonlinear wave equation with nonlinear polarization as a source:

Akira Hasegawa is a theoretical physicist and engineer who has worked in the US and Japan. He is known for his work in the derivation of the Hasegawa–Mima equation, which describes fundamental plasma turbulence and the consequent generation of zonal flow that controls plasma diffusion. Hasegawa also made the discovery of optical solitons in glass fibers, a concept that is essential for high speed optical communications.
Alexey Okulov is a Soviet and Russian physicist, the author of pioneering works in laser physics and theoretical physics.
References
- ↑ Alan C. Newell page at the University of Arizona
- ↑ "John Simon Guggenheim Memorial Foundation". Archived from the original on 3 February 2013. Retrieved 11 February 2013.
- ↑ "SIAM". Archived from the original on 7 July 2014. Retrieved 11 February 2013.
- ↑ Newell, Alan C. (1 December 2013). "How Mother Nature forms her patterns". Arizona Daily Star. Retrieved 10 July 2017.