Angenent torus

Last updated

In differential geometry, the Angenent torus is a smooth embedding of the torus into three-dimensional Euclidean space, with the property that it remains self-similar as it evolves under the mean curvature flow. Its existence shows that, unlike the one-dimensional curve-shortening flow (for which every embedded closed curve converges to a circle as it shrinks to a point), the two-dimensional mean-curvature flow has embedded surfaces that form more complex singularities as they collapse.

Differential geometry branch of mathematics

Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra to study problems in geometry. The theory of plane and space curves and surfaces in the three-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century and the 19th century.

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup.

Torus doughnut-shaped surface of revolution

In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution.

Contents

History

The Angenent torus is named after Sigurd Angenent, who published a proof that it exists in 1992. [1] However, as early as 1990, Gerhard Huisken wrote that Matthew Grayson had told him of "numerical evidence" of its existence. [2] [3]

Sigurd Bernardus Angenent is a Dutch-born mathematician and professor at the University of Wisconsin–Madison. Angenent works on partial differential equations and dynamical systems, with his recent research focusing on heat equation and diffusion equation. The Angenent torus and Angenent ovals are special solutions to the mean curvature flow published by Angenent in 1992; the Angenent torus remains self-similar as it collapses to a point under the flow, and the Angenent ovals are the only compact convex ancient solutions other than circles for the curve-shortening flow.

Gerhard Huisken German mathematician

Gerhard Huisken is a German mathematician.

Existence

To prove the existence of the Angenent torus, Angenent first posits that it should be a surface of revolution. Any such surface can be described by its cross-section, a curve on a half-plane (where the boundary line of the half-plane is the axis of revolution of the surface). Following ideas of Huisken, [2] Angenent defines a Riemannian metric on the half-plane, with the property that the geodesics for this metric are exactly the cross-sections of surfaces of revolution that remain self-similar and collapse to the origin after one unit of time. This metric is highly non-uniform, but it has a reflection symmetry, whose symmetry axis is the half-line that passes through the origin perpendicularly to the boundary of the half-plane. [1]

Surface of revolution

A surface of revolution is a surface in Euclidean space created by rotating a curve around an axis of rotation.

Geodesic shortest path between two points on a curved surface

In differential geometry, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". The term "geodesic" comes from geodesy, the science of measuring the size and shape of Earth; in the original sense, a geodesic was the shortest route between two points on the Earth's surface, namely, a segment of a great circle. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

By considering the behavior of geodesics that pass perpendicularly through this axis of reflectional symmetry, at different distances from the origin, and applying the intermediate value theorem, Angenent finds a geodesic that passes through the axis perpendicularly at a second point. This geodesic and its reflection join up to form a simple closed geodesic for the metric on the half-plane. When this closed geodesic is used to make a surface of revolution, it forms the Angenent torus.

Intermediate value theorem theorem

In mathematical analysis, the intermediate value theorem states that if a continuous function, f, with an interval, [a, b], as its domain, takes values f(a) and f(b) at each end of the interval, then it also takes any value between f(a) and f(b) at some point within the interval.

Jordan curve theorem theorem stating that a closed curve divides the plane into two regions

In topology, a Jordan curve, sometimes called a plane simple closed curve, is a non-self-intersecting continuous loop in the plane. The Jordan curve theorem asserts that every Jordan curve divides the plane into an "interior" region bounded by the curve and an "exterior" region containing all of the nearby and far away exterior points, so that every continuous path connecting a point of one region to a point of the other intersects with that loop somewhere. While the statement of this theorem seems to be intuitively obvious, it takes some ingenuity to prove it by elementary means. More transparent proofs rely on the mathematical machinery of algebraic topology, and these lead to generalizations to higher-dimensional spaces.

In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold is a geodesic that returns to its starting point with the same tangent direction. It may be formalized as the projection of a closed orbit of the geodesic flow on the tangent space of the manifold.

Other geodesics lead to other surfaces of revolution that remain self-similar under the mean-curvature flow, including spheres, cylinders, planes, and (according to numerical evidence but not rigorous proof) immersed topological spheres with multiple self-crossings. [1] Kleene & Møller (2014) prove that the only complete smooth embedded surfaces of rotation that stay self-similar under the mean curvature flow are planes, cylinders, spheres, and topological tori. They conjecture more strongly that the Angenent torus is the only torus with this property. [4]

Immersion (mathematics) differentiable function whose derivative is everywhere injective

In mathematics, an immersion is a differentiable function between differentiable manifolds whose derivative is everywhere injective. Explicitly, f : M → N is an immersion if

Applications

The Angenent torus can be used to prove the existence of certain other kinds of singularities of the mean curvature flow. For instance, if a dumbbell shaped surface, consisting of a thin cylindrical "neck" connecting two large volumes, can have its neck surrounded by a disjoint Angenent torus, then the two surfaces of revolution will remain disjoint under the mean curvature flow until one of them reaches a singularity; if the ends of the dumbbell are large enough, this implies that the neck must pinch off, separating the two spheres from each other, before the torus surrounding the neck collapses. [1] [5]

Dumbbell piece of equipment used in weight training

The dumbbell, a type of free weight, is a piece of equipment used in weight training. It can be used individually or in pairs, with one in each hand

Any shape that stays self-similar but shrinks under the mean curvature flow forms an ancient solution to the flow, one that can be extrapolated backwards for all time. However, the reverse is not true. In the same paper in which he published the Angenent torus, Angenent also described the Angenent ovals; these are not self-similar, but they are the only simple closed curves in the plane, other than a circle, that give ancient solutions to the curve-shortening flow. [1] [6]

Related Research Articles

Surface (topology) two-dimensional manifold, and, as such, may be an "abstract surface" not embedded in any Euclidean space

In topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

Möbius strip Two-dimensional surface with only one side and only one edge

A Möbius strip, Möbius band, or Möbius loop, also spelled Mobius or Moebius, is a surface with only one side and only one boundary. The Möbius strip has the mathematical property of being unorientable. It can be realized as a ruled surface. Its discovery is attributed to the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858, though a structure similar to the Möbius strip can be seen in Roman mosaics dated circa 200–250 AD.

Curvature physical quantity

In mathematics, curvature is any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object such as a surface deviates from being a flat plane, or a curve from being straight as in the case of a line, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space – in a way that relates to the radius of curvature of circles that touch the object – and intrinsic curvature, which is defined in terms of the lengths of curves within a Riemannian manifold.

Gaussian curvature

In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a surface at a point is the product of the principal curvatures, κ1 and κ2, at the given point:

Ricci flow intrinsic geometric flow

In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric.

In mathematics, spaces of non-positive curvature occur in many contexts and form a generalization of hyperbolic geometry. In the category of Riemannian manifolds, one can consider the sectional curvature of the manifold and require that this curvature be everywhere less than or equal to zero. The notion of curvature extends to the category of geodesic metric spaces, where one can use comparison triangles to quantify the curvature of a space; in this context, non-positively curved spaces are known as (locally) CAT(0) spaces.

In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold. Intuitively, a family of surfaces evolves under mean curvature flow if the normal component of the velocity of which a point on the surface moves is given by the mean curvature of the surface. For example, a round sphere evolves under mean curvature flow by shrinking inward uniformly. Except in special cases, the mean curvature flow develops singularities.

In mathematics, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature. They can be interpreted as flows on a moduli space or a parameter space.

Differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.

In the field of differential geometry in mathematics, inverse mean curvature flow (IMCF) is an example of a geometric flow of hypersurfaces of a Riemannian manifold. Intuitively, a family of surfaces evolves under IMCF if the outward normal speed at which a point on the surface moves is given by the reciprocal of the mean curvature of the surface. For example, a round sphere evolves under IMCF by expanding outward uniformly at an exponentially growing rate. In general, this flow does not exist, and even if it does, it generally develops singularities. Nevertheless, it has recently been an important tool in differential geometry and mathematical problems in general relativity.

The Geometry Festival is an annual mathematics conference held in the United States.

In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form. These concepts were put in their current form with principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.

Simon Brendle German mathematician

Simon Brendle is a German mathematician working in differential geometry and nonlinear partial differential equations. He received his Ph.D. from Tübingen University under the supervision of Gerhard Huisken (2001). He was a professor at Stanford University (2005–2016), and is currently a professor at Columbia University. He has held visiting positions at MIT, ETH Zürich, Princeton University, and Cambridge University.

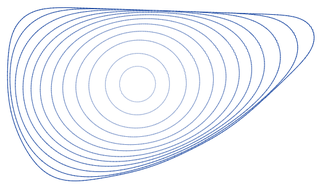
Curve-shortening flow

In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.

In mathematics, the stretch factor of an embedding measures the factor by which the embedding distorts distances. Suppose that one metric space S is embedded into another metric space T by a metric map, a continuous one-to-one function f that preserves or reduces the distance between every pair of points. Then the embedding gives rise to two different notions of distance between pairs of points in S. Any pair of points (x,y) in S has both an intrinsic distance, the distance from x to y in S, and a smaller extrinsic distance, the distance from f(x) to f(y) in T. The stretch factor of the pair is the ratio between these two distances, d(x,y)/d(f ,f ). The stretch factor of the whole mapping is the supremum of the stretch factors of all pairs of points. The stretch factor has also been called the distortion or dilation of the mapping.

In differential geometry, Huisken's monotonicity formula states that, if an n-dimensional surface in (n + 1)-dimensional Euclidean space undergoes the mean curvature flow, then its convolution with an appropriately scaled and time-reversed heat kernel is non-increasing. The result is named after Gerhard Huisken, who published it in 1990.

References

  1. 1 2 3 4 5 Angenent, Sigurd B. (1992), "Shrinking doughnuts" (PDF), Nonlinear diffusion equations and their equilibrium states, 3 (Gregynog, 1989), Progress in Nonlinear Differential Equations and their Applications, 7, Boston, MA: Birkhäuser, pp. 21–38, MR   1167827 .
  2. 1 2 Huisken, Gerhard (1990), "Asymptotic behavior for singularities of the mean curvature flow", Journal of Differential Geometry, 31 (1): 285–299, MR   1030675 .
  3. ↑ Mantegazza, Carlo (2011), Lecture notes on mean curvature flow, Progress in Mathematics, 290, Basel: Birkhäuser/Springer, p. 14, doi:10.1007/978-3-0348-0145-4, ISBN   978-3-0348-0144-7, MR   2815949 .
  4. ↑ Kleene, Stephen; Møller, Niels Martin (2014), "Self-shrinkers with a rotational symmetry", Transactions of the American Mathematical Society, 366 (8): 3943–3963, arXiv: 1008.1609  Lock-green.svg, doi:10.1090/S0002-9947-2014-05721-8, MR   3206448 .
  5. ↑ Ecker, Klaus (2004), Regularity theory for mean curvature flow, Progress in Nonlinear Differential Equations and their Applications, 57, Boston, MA: Birkhäuser, p. 29, doi:10.1007/978-0-8176-8210-1, ISBN   0-8176-3243-3, MR   2024995 .
  6. ↑ Daskalopoulos, Panagiota; Hamilton, Richard; Sesum, Natasa (2010), "Classification of compact ancient solutions to the curve shortening flow", Journal of Differential Geometry, 84 (3): 455–464, arXiv: 0806.1757  Lock-green.svg, MR   2669361 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.