 | This article needs additional citations for verification .(January 2010) |
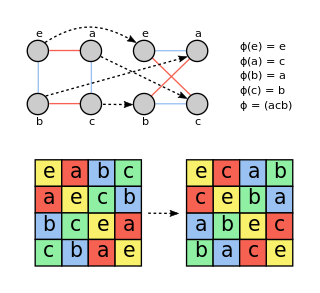
In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is a bijective antihomomorphism, i.e. an antiisomorphism, from a set to itself. From bijectivity it follows that antiautomorphisms have inverses, and that the inverse of an antiautomorphism is also an antiautomorphism.
Informally, an antihomomorphism is a map that switches the order of multiplication. Formally, an antihomomorphism between structures and is a homomorphism , where equals as a set, but has its multiplication reversed to that defined on . Denoting the (generally non-commutative) multiplication on by , the multiplication on , denoted by , is defined by . The object is called the opposite object to (respectively, opposite group , opposite algebra , opposite category etc.).
This definition is equivalent to that of a homomorphism (reversing the operation before or after applying the map is equivalent). Formally, sending to and acting as the identity on maps is a functor (indeed, an involution).
In group theory, an antihomomorphism is a map between two groups that reverses the order of multiplication. So if φ : X → Y is a group antihomomorphism,
for all x, y in X.
The map that sends x to x−1 is an example of a group antiautomorphism. Another important example is the transpose operation in linear algebra, which takes row vectors to column vectors. Any vector-matrix equation may be transposed to an equivalent equation where the order of the factors is reversed.
With matrices, an example of an antiautomorphism is given by the transpose map. Since inversion and transposing both give antiautomorphisms, their composition is an automorphism. This involution is often called the contragredient map, and it provides an example of an outer automorphism of the general linear group GL(n, F), where F is a field, except when |F| = 2 and n = 1 or 2, or |F| = 3 and n = 1 (i.e., for the groups GL(1, 2), GL(2, 2), and GL(1, 3)).
In ring theory, an antihomomorphism is a map between two rings that preserves addition, but reverses the order of multiplication. So φ : X → Y is a ring antihomomorphism if and only if:
for all x, y in X. [1]
For algebras over a field K, φ must be a K-linear map of the underlying vector space. If the underlying field has an involution, one can instead ask φ to be conjugate-linear, as in conjugate transpose, below.
It is frequently the case that antiautomorphisms are involutions, i.e. the square of the antiautomorphism is the identity map; these are also called involutive antiautomorphisms. For example, in any group the map that sends x to its inverse x−1 is an involutive antiautomorphism.
A ring with an involutive antiautomorphism is called a *-ring, and these form an important class of examples.
If the source X or the target Y is commutative, then an antihomomorphism is the same thing as a homomorphism.
The composition of two antihomomorphisms is always a homomorphism, since reversing the order twice preserves order. The composition of an antihomomorphism with a homomorphism gives another antihomomorphism.
In mathematics, an associative algebraA is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In mathematics, a group action on a space is a group homomorphism of a given group into the group of transformations of the space. Similarly, a group action on a mathematical structure is a group homomorphism of a group into the automorphism group of the structure. It is said that the group acts on the space or structure. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn in it. In particular, it acts on the set of all triangles. Similarly, the group of symmetries of a polyhedron acts on the vertices, the edges, and the faces of the polyhedron.
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the Ancient Greek language: ὁμός meaning "same" and μορφή meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925).
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσοςisos "equal", and μορφήmorphe "form" or "shape".
In mathematics, a Lie group is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract, generic concept of multiplication and the taking of inverses (division). Combining these two ideas, one obtains a continuous group where points can be multiplied together, and their inverse can be taken. If, in addition, the multiplication and taking of inverses are defined to be smooth (differentiable), one obtains a Lie group.
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. Since there are such permutation operations, the order of the symmetric group is .
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed, this intuition can be formalized to define so-called functor categories. Natural transformations are, after categories and functors, one of the most fundamental notions of category theory and consequently appear in the majority of its applications.
In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, the complex conjugate of is equal to The complex conjugate of is often denoted as
Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.
In mathematics, and more specifically in abstract algebra, a *-algebra is a mathematical structure consisting of two involutive ringsR and A, where R is commutative and A has the structure of an associative algebra over R. Involutive algebras generalize the idea of a number system equipped with conjugation, for example the complex numbers and complex conjugation, matrices over the complex numbers and conjugate transpose, and linear operators over a Hilbert space and Hermitian adjoints. However, it may happen that an algebra admits no involution at all.
In mathematics, an involution, involutory function, or self-inverse function is a function f that is its own inverse,
In algebra, a module homomorphism is a function between modules that preserves the module structures. Explicitly, if M and N are left modules over a ring R, then a function is called an R-module homomorphism or an R-linear map if for any x, y in M and r in R,
In category theory, two categories C and D are isomorphic if there exist functors F : C → D and G : D → C which are mutually inverse to each other, i.e. FG = 1D and GF = 1C. This means that both the objects and the morphisms of C and D stand in a one-to-one correspondence to each other. Two isomorphic categories share all properties that are defined solely in terms of category theory; for all practical purposes, they are identical and differ only in the notation of their objects and morphisms.
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. Such involutions sometimes have fixed points, so that the dual of A is A itself. For example, Desargues' theorem is self-dual in this sense under the standard duality in projective geometry.
In mathematics, the spin representations are particular projective representations of the orthogonal or special orthogonal groups in arbitrary dimension and signature. More precisely, they are representations of the spin groups, which are double covers of the special orthogonal groups. They are usually studied over the real or complex numbers, but they can be defined over other fields.
In mathematics, particularly in abstract algebra, a semigroup with involution or a *-semigroup is a semigroup equipped with an involutive anti-automorphism, which—roughly speaking—brings it closer to a group because this involution, considered as unary operator, exhibits certain fundamental properties of the operation of taking the inverse in a group: uniqueness, double application "cancelling itself out", and the same interaction law with the binary operation as in the case of the group inverse. It is thus not a surprise that any group is a semigroup with involution. However, there are significant natural examples of semigroups with involution that are not groups.
In mathematics, the complexification or universal complexification of a real Lie group is given by a continuous homomorphism of the group into a complex Lie group with the universal property that every continuous homomorphism of the original group into another complex Lie group extends compatibly to a complex analytic homomorphism between the complex Lie groups. The complexification, which always exists, is unique up to unique isomorphism. Its Lie algebra is a quotient of the complexification of the Lie algebra of the original group. They are isomorphic if the original group has a quotient by a discrete normal subgroup which is linear.
In mathematics, Lie group–Lie algebra correspondence allows one to correspond a Lie group to a Lie algebra or vice versa, and study the conditions for such a relationship. Lie groups that are isomorphic to each other have Lie algebras that are isomorphic to each other, but the converse is not necessarily true. One obvious counterexample is and which are non-isomorphic to each other as Lie groups but their Lie algebras are isomorphic to each other. However, by restricting our attention to the simply connected Lie groups, the Lie group-Lie algebra correspondence will be one-to-one.
