In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities. The orientation of an object's acceleration is given by the orientation of the net force acting on that object. The magnitude of an object's acceleration, as described by Newton's Second Law, is the combined effect of two causes:
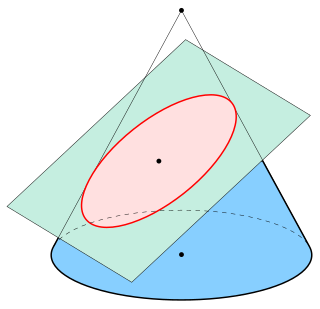
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .
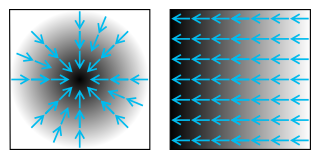
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field whose value at a point is the vector whose components are the partial derivatives of at . That is, for , its gradient is defined at the point in n-dimensional space as the vector:

In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest.

In Newtonian mechanics, linear momentum, translational momentum, or simply momentum is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If m is an object's mass and v is its velocity, then the object's momentum is

Nuclear fusion is a reaction in which two or more atomic nuclei are combined to form one or more different atomic nuclei and subatomic particles. The difference in mass between the reactants and products is manifested as either the release or the absorption of energy. This difference in mass arises due to the difference in atomic binding energy between the nuclei before and after the reaction. Fusion is the process that powers active or main sequence stars and other high-magnitude stars, where large amounts of energy are released.
In physics, power is the amount of energy transferred or converted per unit time. In the International System of Units, the unit of power is the watt, equal to one joule per second. In older works, power is sometimes called activity. Power is a scalar quantity.

In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
- The laws of physics are invariant in all inertial frames of reference.
- The speed of light in vacuum is the same for all observers, regardless of the motion of the light source or observer.

In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Objects that tensors may map between include vectors and scalars, and even other tensors. There are many types of tensors, including scalars and vectors, dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system.

Voltage, electric potential difference, electric pressure or electric tension is the difference in electric potential between two points, which is defined as the work needed per unit of charge to move a test charge between the two points. In the International System of Units, the derived unit for voltage is named volt. In SI units, work per unit charge is expressed as joules per coulomb, where 1 volt = 1 joule per 1 coulomb. The old SI definition for volt used power and current; starting in 1990, the quantum Hall and Josephson effect were used, and recently (2019) fundamental physical constants have been introduced for the definition of all SI units and derived units. Voltage or electric potential difference is denoted symbolically by ∆V, simplified V, or U, for instance in the context of Ohm's or Kirchhoff's circuit laws.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form:

In physics, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, it is often represented as the product of force and displacement. A force is said to do positive work if it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.

In biochemistry, Michaelis–Menten kinetics is one of the best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating reaction rate to , the concentration of a substrate S. Its formula is given by

In physics and relativity, time dilation is the difference in the elapsed time as measured by two clocks. It is either due to a relative velocity between them or to a difference in gravitational potential between their locations. When unspecified, "time dilation" usually refers to the effect due to velocity.
This gallery of sovereign state flags shows the national or state flags of sovereign states that appear on the list of sovereign states. For other flags, please see flags of active autonomist and secessionist movements, flags of extinct states and gallery of flags of dependent territories. Each flag is depicted as if the flagpole is positioned on the left of the flag, except for those of Iran, Iraq and Saudi Arabia which are depicted with the hoist to the right.
In linear algebra, an eigenvector or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by , is the factor by which the eigenvector is scaled.

A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals.

Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical mechanics, if the present state is known, it is possible to predict how it will move in the future (determinism), and how it has moved in the past (reversibility).

The velocity of an object is the rate of change of its position with respect to a frame of reference, and is a function of time. Velocity is equivalent to a specification of an object's speed and direction of motion. Velocity is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of bodies.