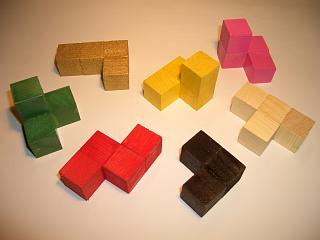A burr puzzle is an interlocking puzzle consisting of notched sticks, combined to make one three-dimensional, usually symmetrical unit. These puzzles are traditionally made of wood, but versions made of plastic or metal can also be found. Quality burr puzzles are usually precision-made for easy sliding and accurate fitting of the pieces. In recent years the definition of "burr" is expanding, as puzzle designers use this name for puzzles not necessarily of stick-based pieces.
The term "burr" is first mentioned in a 1928 book by Edwin Wyatt, [1] but the text implies that it was commonly used before. The term is attributed to the finished shape of many of these puzzles, resembling a seed burr. The origin of burr puzzles is unknown. The first known record [2] appears in a 1698 engraving used as a frontispiece page of Chambers's Cyclopaedia. [3] [ better source needed ] Later records can be found in German catalogs from the late 18th century and early 19th century. [4] There are claims of the burr being a Chinese invention, like other classic puzzles such as the Tangram. [5] In Kerala, India, these wooden puzzles are called edakoodam(ഏടാകൂടം). [6] [7]
The six-piece burr, also called "Puzzle Knot" or "Chinese Cross", is the most well-known and presumably the oldest of the burr puzzles. This is actually a family of puzzles, all sharing the same finished shape and basic shape of the pieces. The earliest US patent for a puzzle of this kind dates back to 1917. [8]
For many years, the six-piece burr was very common and popular, but was considered trite and uninteresting by enthusiasts. Most of the puzzles made and sold were very similar to one another and most of them included a "key" piece, an unnotched stick that slides easily out. In the late 1970s, however, the six-piece burr regained the attention of inventors and collectors, thanks largely to a computer analysis conducted by the mathematically trained puzzle designer Bill Cutler which was published by Martin Gardner in his Mathematical Games column in Scientific American. [9]
All six pieces of the puzzle are square sticks of equal length (at least 3 times their width). When solved, the pieces are arranged in three perpendicular, mutually intersecting pairs. The notches of all sticks are located within the region of intersection, so when the puzzle is assembled they are unseen. All notches can be described as being made by removing cubic units (with an edge length of half the sticks' width), as shown in the figure:
There are 12 removable cubic units, and different puzzles of this family are made of sticks with different units removed. 4,096 permutations exist for removing the cubic units. Of those, we ignore the ones that cut the stick in two and the ones creating identical pieces, and are left with 837 usable pieces. [10] Theoretically, these pieces can be combined to create over 35 billion possible assemblies, but it is estimated that fewer than six billion of them are actual puzzles, capable of being assembled or taken apart. [11]
A burr puzzle with no internal voids when assembled is called a solid burr. These burrs can be taken apart directly by removing a piece or some pieces in one move. Up until the late 1970s, solid burrs received the most attention and publications referred only to this type. [13] 119,979 solid burrs are possible, using 369 of the usable pieces. To assemble all these puzzles, one would need a set of 485 pieces, as some of the puzzles include identical pieces. [10]
For aesthetic, but mostly practical reasons, the burr pieces can be divided into three types:
59 of the usable pieces are notchable, including the unnotched stick. Of those, only 25 can be used to create solid burrs. This set, often referred to as "The 25 notchable pieces", with the addition of 17 duplicates, can be assembled to create 221 different solid burr puzzles. Some of those puzzles have more than one solution, for a total of 314 solutions. These pieces are very popular, and full sets are manufactured and sold by many companies.
For all solid burrs, one movement is required to remove the first piece or pieces. However, a holey burr, which has internal voids when assembled, can require more than one move. The number of moves required for removing the first piece is referred to as the level of the burr. All solid burrs are therefore level 1. The higher the level is, the more difficult the puzzle.
During the 1970s and 1980s, attempts were made by experts to find burrs of an ever-higher level. On 1979, the American designer and craftsman Stewart Coffin found a level-3 puzzle. In 1985, Bill Cutler found a level-5 burr [14] and shortly afterwards a level-7 burr was found by the Israeli Philippe Dubois. [13] In 1990, Cutler completed the final part of his analysis and found that the highest possible level using notchable pieces is 5, and 139 of those puzzles exist. The highest level possible for a six-piece burr with more than one solution is 12, meaning 12 moves are required to remove the first piece. [11]
A three-piece burr made from sticks with "regular" right-angled notches (as the six-piece burr), cannot be assembled or taken apart. [15] There are, however, some three-piece burrs with different kinds of notches, the best known of them being the one mentioned by Wyatt in his 1928 book, consisting of a rounded piece that is meant to be rotated. [1]
The Altekruse puzzle is named after the grantee of its 1890 patent, though the puzzle is of earlier origin. [16] The name "Altekruse" is of Austrian-German origin and means "old-cross" in German, which led to the presumption that it was a pseudonym, but a man by that name immigrated to America in 1844 with his three brothers to avoid being drafted to the Prussian Army and is presumed to be the one who filed this patent. [17]
A classic Altekruse consists of 12 identical pieces. In order to disassemble it, two halves of the puzzle have to be moved in opposite directions. Using two more of these pieces, the puzzle can be assembled in a different way. By the same principle, other puzzles of this family can be created, with 6, 24, 36 and so forth. Despite their size, those bigger puzzles are not considered very difficult, yet they require patience and dexterity to assemble.
The Chuck puzzle was invented and patented by Edward Nelson in 1897. [18] His design was improved and developed by Ron Cook of the British company Pentangle Puzzles who designed other puzzles of the family. [19]
The Chuck consists mostly of U-shaped stick pieces of various lengths, and some with an extra notch that are used as key pieces. For creating bigger Chuck puzzles (named Papa-chuck, Grandpapachuck and Great Grandpapachuck, by Cook) one would need to add longer pieces. The Chuck can also be regarded as an extension of a six-piece burr of very simple pieces called Baby-chuck, which is very easy to solve. Chuck pieces of different lengths can also be used to create asymmetric shapes, assembled according to the same principle as the original puzzle.
The origin of the Pagoda, also called "Japanese Crystal" is unknown. It is mentioned in Wyatt's 1928 book. [1] Puzzles of this family can be regarded as an extension of the "three-piece burr" (Pagoda of size 1), however they do not require special notches to be assembled or taken apart. Pagoda of size 2 consists of 9 pieces, and bigger versions consist of 19, 33, 51 and so forth. Pagoda of size consists of pieces.
Though most burr puzzle pieces are made with square notches, some are made with diagonal notches. Diagonal burr pieces are square sticks with V-shaped notches, cut at an angle of 45° off the stick's face. These puzzles are often called "stars", as it is customary to also cut the sticks' edges at an angle of 45°, for aesthetic reasons, giving the assembled puzzle a star-like shape.
Samuel Loyd was an American chess player, chess composer, puzzle author, and recreational mathematician. Loyd was born in Philadelphia but raised in New York City.
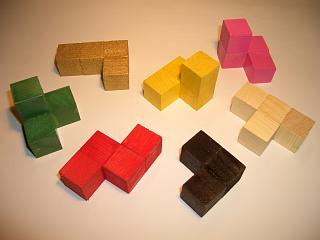
The Soma cube is a solid dissection puzzle invented by Danish polymath Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg.
The tangram is a dissection puzzle consisting of seven flat polygons, called tans, which are put together to form shapes. The objective is to replicate a pattern generally found in a puzzle book using all seven pieces without overlap. Alternatively the tans can be used to create original minimalist designs that are either appreciated for their inherent aesthetic merits or as the basis for challenging others to replicate its outline. It is reputed to have been invented in China sometime around the late 18th century and then carried over to America and Europe by trading ships shortly after. It became very popular in Europe for a time, and then again during World War I. It is one of the most widely recognized dissection puzzles in the world and has been used for various purposes including amusement, art, and education.
A jigsaw puzzle is a tiling puzzle that requires the assembly of often irregularly shaped interlocking and mosaicked pieces, each of which typically has a portion of a picture. When assembled, the puzzle pieces produce a complete picture.
A mechanical puzzle is a puzzle presented as a set of mechanically interlinked pieces in which the solution is to manipulate the whole object or parts of it. While puzzles of this type have been in use by humanity as early as the 3rd century BC, one of the most well-known mechanical puzzles of modern day is the Rubik's Cube, invented by the Hungarian architect Ernő Rubik in 1974. The puzzles are typically designed for a single player, where the goal is for the player to see through the principle of the object, rather than accidentally coming up with the right solution through trial and error. With this in mind, they are often used as an intelligence test or in problem solving training.
Disentanglement puzzles are a type or group of mechanical puzzle that involves disentangling one piece or set of pieces from another piece or set of pieces. Several subtypes are included under this category, the names of which are sometimes used synonymously for the group: wire puzzles; nail puzzles; ring-and-string puzzles; et al. Although the initial object is disentanglement, the reverse problem of reassembling the puzzle can be as hard as—or even harder than—disentanglement. There are several different kinds of disentanglement puzzles, though a single puzzle may incorporate several of these features.
Pick-up sticks, pick-a-stick, jackstraws, jack straws, spillikins, spellicans, or fiddlesticks is a game of physical and mental skill in which a bundle of sticks, between 8 and 20 centimeters long, is dropped as a loose bunch onto a table top into a random pile. Each player, in turn, tries to remove a stick from the pile without disturbing any of the others. The object of the game is to pick up the most sticks or to score the most points based on the color of the sticks.
Frame and panel construction, also called rail and stile, is a woodworking technique often used in the making of doors, wainscoting, and other decorative features for cabinets, furniture, and homes. The basic idea is to capture a 'floating' panel within a sturdy frame, as opposed to techniques used in making a slab solid wood cabinet door or drawer front, the door is constructed of several solid wood pieces running in a vertical or horizontal direction with exposed endgrains. Usually, the panel is not glued to the frame but is left to 'float' within it so that seasonal movement of the wood comprising the panel does not distort the frame.
A dissection puzzle, also called a transformation puzzle or Richter puzzle, is a tiling puzzle where a set of pieces can be assembled in different ways to produce two or more distinct geometric shapes. The creation of new dissection puzzles is also considered to be a type of dissection puzzle. Puzzles may include various restraints, such as hinged pieces, pieces that can fold, or pieces that can twist. Creators of new dissection puzzles emphasize using a minimum number of pieces, or creating novel situations, such as ensuring that every piece connects to another with a hinge.
Stick puzzles are a type of combination puzzle that uses multiple sticks or 'polysticks' to assemble two- or three-dimensional configurations.
In woodworking and carpentry, a pair of winding sticks is a tool that aids in viewing twist in pieces of lumber by amplifying the defect. Winding sticks can be as simple as any two straight sticks or they can be elegant, decorated, dimensionally stable wood like mahogany. A pair of framing squares may also be suitable. Traditionally they are 16 inches (41 cm) to 30 inches (76 cm) long, 1+3⁄4 inches (44 mm) tall and tapered in their height from 3⁄8 inch (9.5 mm) to 1⁄8 inch (3.2 mm). The longer the winding sticks, the more they will amplify the wind. It is common for a woodworker to make a matching pair for the purpose, and contrasting colors of woods improve the discernability of differences in height and level between the two sticks as they are compared.
Gess is an abstract strategy board game for two players, involving a grid board and mutating pieces. The name was chosen as a conflation of "chess" and "Go". It is pronounced with a hard "g" as in "Go", and is thus homophonous with "guess".
The T puzzle is a tiling puzzle consisting of four polygonal shapes which can be put together to form a capital T. The four pieces are usually one isosceles right triangle, two right trapezoids and an irregular shaped pentagon.
The diabolical cube is a three-dimensional dissection puzzle consisting of six polycubes that can be assembled together to form a single 3 × 3 × 3 cube. The six pieces are: one dicube, one tricube, one tetracube, one pentacube, one hexacube and one heptacube, that is, polycubes of 2, 3, 4, 5, 6 and 7 cubes.
Puzzle Pirates is a massively multiplayer online game developed by Three Rings Design. The player takes the role of a pirate, adventuring on the high seas and pillaging money from roaming enemy ships. The mechanics of Puzzle Pirates are driven by puzzles. For example, to effectively sail a ship, players must play puzzle games representing work at the sails for speed, pumping bilge water to remove it from the ship, and carpentry to fix any damage the ship may take.
The Crown of Thorns is a woodworking technique of tramp art using interlocking wooden pieces that are notched to intersect at right angles forming joints and self-supporting objects, objects that have a "prickly" and transparent quality. Common examples include wreath-shaped picture frames that look similar to Jesus' "crown of thorns".
A tally stick was an ancient memory aid device used to record and document numbers, quantities and messages. Tally sticks first appear as animal bones carved with notches during the Upper Palaeolithic; a notable example is the Ishango Bone. Historical reference is made by Pliny the Elder about the best wood to use for tallies, and by Marco Polo (1254–1324) who mentions the use of the tally in China. Tallies have been used for numerous purposes such as messaging and scheduling, and especially in financial and legal transactions, to the point of being currency.
The Altekruse Puzzle is a type of burr puzzle invented by Austrian inventor William Altekruse.
Stewart Coffin is an American puzzle maker. According to Ars Technica, he is considered to be one of the "best designers of polyhedral interlocking puzzles in the world."
The second season of The Challenge: All Stars premiered on Paramount+ on November 11, 2021. The season features twenty-four past cast members from the main series competing for $500,000.
Media related to Burr puzzles at Wikimedia Commons
