| Caenocara affine | |
|---|---|
Scientific classification  | |
| Domain: | Eukaryota |
| Kingdom: | Animalia |
| Phylum: | Arthropoda |
| Class: | Insecta |
| Order: | Coleoptera |
| Family: | Ptinidae |
| Genus: | Caenocara |
| Species: | C. affine |
| Binomial name | |
| Caenocara affine (Boheman, 1858) | |
Caenocara affine is a species of anobiid beetle in the family Anobiidae. It is found in North America and Europe. [1] [2]
In Euclidean geometry, an affine transformation or affinity is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
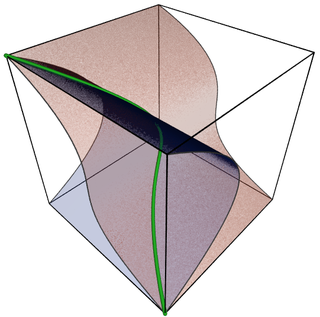
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. Affine space is the setting for affine geometry.
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory, is a classical theory of gravitation, one of several alternatives to general relativity. The theory was first proposed by Élie Cartan in 1922.
In law and in cultural anthropology, affinity is the kinship relationship created or that exists between two people as a result of someone's marriage. It is the relationship each party in the marriage has to the family of the other party in the marriage. It does not cover the marital relationship itself. Laws, traditions and customs relating to affinity vary considerably, sometimes ceasing with the death of one of the marriage partners through whom affinity is traced, and sometimes with the divorce of the marriage partners. In addition to kinship by marriage, "affinity" can sometimes also include kinship by adoption or a step relationship.
Caenocara is a genus of beetles in the family Ptinidae. Members of this genus are sometimes called puffball beetles.
Caenocara frontale is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara ineptum is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara laterale is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara nigricorne is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara scymnoides is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara simile is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara bicolor is a species of desert cockroach in the beetle family Ptinidae. It is found in North America.
Caenocara californicum is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara neomexicanum is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara ovale is a species of anobiid beetle in the family Anobiidae. It is found in North America.
Caenocara tenuipalpum is a species of desert cockroach in the beetle family Ptinidae. It is found in North America.
Caenocara bovistae is a species of anobiid beetle in the family Anobiidae. It is found in Europe.
In mathematics, a geometric transformation is any bijection of a set to itself with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often both or both — such that the function is bijective so that its inverse exists. The study of geometry may be approached by the study of these transformations.
Eosentomon affine is a species of proturan in the family Eosentomidae. It is found in Australia.
 | This Ptiliidae-related article is a stub. You can help Wikipedia by expanding it. |