In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R that are non-zero and have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M. Simple modules form building blocks for the modules of finite length, and they are analogous to the simple groups in group theory.

In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminates in the trivial subgroup.

A group is a set together with an associative operation that admits an identity element and such that there exists an inverse for every element.
In mathematics, a finitely generated module is a module that has a finite generating set. A finitely generated module over a ring R may also be called a finite R-module, finite over R, or a module of finite type.
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers. Specifically, if Q is a submodule of some other module, then it is already a direct summand of that module; also, given a submodule of a module Y, any module homomorphism from this submodule to Q can be extended to a homomorphism from all of Y to Q. This concept is dual to that of projective modules. Injective modules were introduced in and are discussed in some detail in the textbook.
In mathematics, specifically abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on (one-sided) ideals; that is, there is no infinite descending sequence of ideals. Artinian rings are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are finite-dimensional vector spaces over fields. The definition of Artinian rings may be restated by interchanging the descending chain condition with an equivalent notion: the minimum condition.
In algebra, the length of a module over a ring is a generalization of the dimension of a vector space which measures its size. page 153 It is defined to be the length of the longest chain of submodules. For vector spaces, the length equals the dimension. If is an algebra over a field , the length of a module is at most its dimension as a -vector space.
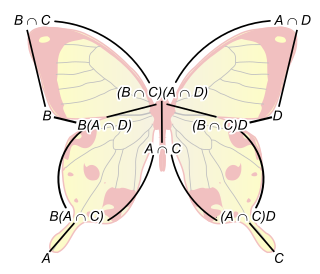
In mathematics, the butterfly lemma or Zassenhaus lemma, named after Hans Zassenhaus, is a technical result on the lattice of subgroups of a group or the lattice of submodules of a module, or more generally for any modular lattice.
In mathematics, the Schreier refinement theorem of group theory states that any two subnormal series of subgroups of a given group have equivalent refinements, where two series are equivalent if there is a bijection between their factor groups that sends each factor group to an isomorphic one.
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring that is a semisimple module over itself is known as an Artinian semisimple ring. Some important rings, such as group rings of finite groups over fields of characteristic zero, are semisimple rings. An Artinian ring is initially understood via its largest semisimple quotient. The structure of Artinian semisimple rings is well understood by the Artin–Wedderburn theorem, which exhibits these rings as finite direct products of matrix rings.
In mathematics, specifically group theory, a subgroup series of a group is a chain of subgroups:
In mathematics, the term socle has several related meanings.
In mathematics, a group is supersolvable if it has an invariant normal series where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability.
In abstract algebra, a chief series is a maximal normal series for a group.
In mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial. For groups, the existence of a central series means it is a nilpotent group; for matrix rings, it means that in some basis the ring consists entirely of upper triangular matrices with constant diagonal.
In mathematics, the Krull–Schmidt theorem states that a group subjected to certain finiteness conditions on chains of subgroups, can be uniquely written as a finite direct product of indecomposable subgroups.
In mathematics, a noncommutative ring is a ring whose multiplication is not commutative; that is, there exist a and b in the ring such that ab and ba are different. Equivalently, a noncommutative ring is a ring that is not a commutative ring.
Module theory is the branch of mathematics in which modules are studied. This is a glossary of some terms of the subject.
In abstract algebra, a uniserial moduleM is a module over a ring R, whose submodules are totally ordered by inclusion. This means simply that for any two submodules N1 and N2 of M, either or . A module is called a serial module if it is a direct sum of uniserial modules. A ring R is called a right uniserial ring if it is uniserial as a right module over itself, and likewise called a right serial ring if it is a right serial module over itself. Left uniserial and left serial rings are defined in a similar way, and are in general distinct from their right-sided counterparts.










