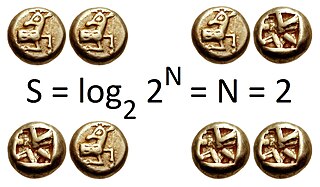In mathematics, convolution is a mathematical operation on two functions that produces a third function. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result. Graphically, it expresses how the 'shape' of one function is modified by the other.
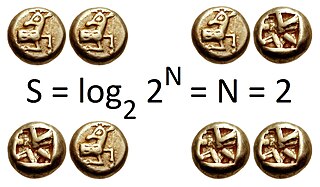
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable , which takes values in the set and is distributed according to , the entropy is where denotes the sum over the variable's possible values. The choice of base for , the logarithm, varies for different applications. Base 2 gives the unit of bits, while base e gives "natural units" nat, and base 10 gives units of "dits", "bans", or "hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable.

A normal distribution or Gaussian distribution is a concept used in probability theory and statistics. It has two descriptive measures: the mean and the standard deviation. If the data being analyzed follows a normal distribution, then about 68% of the observations will fall within one standard deviation of the mean, about 95% will fall within 2 standard deviations, and about 99.7% will fall within 3 standard deviations of the mean.

In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the distribution of a normalized version of the sample mean converges to a standard normal distribution. This holds even if the original variables themselves are not normally distributed. There are several versions of the CLT, each applying in the context of different conditions.

In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts.

In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables, each of which clusters around a mean value.
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces.
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis.

In probability theory and statistics, the Laplace distribution is a continuous probability distribution named after Pierre-Simon Laplace. It is also sometimes called the double exponential distribution, because it can be thought of as two exponential distributions spliced together along the abscissa, although the term is also sometimes used to refer to the Gumbel distribution. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at an exponentially distributed random time. Increments of Laplace motion or a variance gamma process evaluated over the time scale also have a Laplace distribution.
In mathematical statistics, the Kullback–Leibler (KL) divergence, denoted , is a type of statistical distance: a measure of how one reference probability distribution P is different from a second probability distribution Q. Mathematically, it is defined as

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
In statistics and information theory, a maximum entropy probability distribution has entropy that is at least as great as that of all other members of a specified class of probability distributions. According to the principle of maximum entropy, if nothing is known about a distribution except that it belongs to a certain class, then the distribution with the largest entropy should be chosen as the least-informative default. The motivation is twofold: first, maximizing entropy minimizes the amount of prior information built into the distribution; second, many physical systems tend to move towards maximal entropy configurations over time.
In probability theory, calculation of the sum of normally distributed random variables is an instance of the arithmetic of random variables.
Differential entropy is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy of a random variable, to continuous probability distributions. Unfortunately, Shannon did not derive this formula, and rather just assumed it was the correct continuous analogue of discrete entropy, but it is not. The actual continuous version of discrete entropy is the limiting density of discrete points (LDDP). Differential entropy is commonly encountered in the literature, but it is a limiting case of the LDDP, and one that loses its fundamental association with discrete entropy.
In mathematics, a π-system on a set is a collection of certain subsets of such that
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space , closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces. Gaussian measures are named after the German mathematician Carl Friedrich Gauss. One reason why Gaussian measures are so ubiquitous in probability theory is the central limit theorem. Loosely speaking, it states that if a random variable is obtained by summing a large number of independent random variables with variance 1, then has variance and its law is approximately Gaussian.
In mathematics, in particular in measure theory, a content is a real-valued function defined on a collection of subsets such that
An -superprocess, , within mathematics probability theory is a stochastic process on that is usually constructed as a special limit of near-critical branching diffusions.
In mathematics, especially measure theory, a set function is a function whose domain is a family of subsets of some given set and that (usually) takes its values in the extended real number line which consists of the real numbers and
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product is a product distribution.