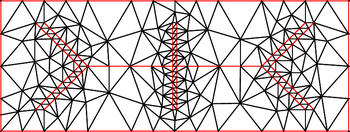
In computational geometry, a Delaunay triangulation or Delone triangulation of a set of points in the plane subdivides their convex hull into triangles whose circumcircles do not contain any of the points. This maximizes the size of the smallest angle in any of the triangles, and tends to avoid sliver triangles.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information".

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.
In geometry, a triangulation is a subdivision of a planar object into triangles, and by extension the subdivision of a higher-dimension geometric object into simplices. Triangulations of a three-dimensional volume would involve subdividing it into tetrahedra packed together.

In computer graphics, a triangulated irregular network (TIN) is a representation of a continuous surface consisting entirely of triangular facets, used mainly as Discrete Global Grid in primary elevation modeling.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.
In computer graphics, marching squares is an algorithm that generates contours for a two-dimensional scalar field. A similar method can be used to contour 2D triangle meshes.

In computational geometry, a Pitteway triangulation is a point set triangulation in which the nearest neighbor of any point p within the triangulation is one of the vertices of the triangle containing p. Alternatively, it is a Delaunay triangulation in which each internal edge crosses its dual Voronoi diagram edge. Pitteway triangulations are named after Michael Pitteway, who studied them in 1973. Not every point set supports a Pitteway triangulation. When such a triangulation exists it is a special case of the Delaunay triangulation, and consists of the union of the Gabriel graph and convex hull.
In computational geometry, the Bowyer–Watson algorithm is a method for computing the Delaunay triangulation of a finite set of points in any number of dimensions. The algorithm can be also used to obtain a Voronoi diagram of the points, which is the dual graph of the Delaunay triangulation.
Parallel mesh generation in numerical analysis is a new research area between the boundaries of two scientific computing disciplines: computational geometry and parallel computing. Parallel mesh generation methods decompose the original mesh generation problem into smaller subproblems which are solved (meshed) in parallel using multiple processors or threads. The existing parallel mesh generation methods can be classified in terms of two basic attributes:
- the sequential technique used for meshing the individual subproblems and
- the degree of coupling between the subproblems.
Jump-and-Walk is an algorithm for point location in triangulations. Surprisingly, the algorithm does not need any preprocessing or complex data structures except some simple representation of the triangulation itself. The predecessor of Jump-and-Walk was due to Lawson (1977) and Green and Sibson (1978), which picks a random starting point S and then walks from S toward the query point Q one triangle at a time. But no theoretical analysis was known for these predecessors until after mid-1990s.

Herbert Edelsbrunner is a computer scientist working in the field of computational geometry, the Arts & Science Professor of Computer Science and Mathematics at Duke University, Professor at the Institute of Science and Technology Austria (ISTA), and the co-founder of Geomagic, Inc. He was the first of only three computer scientists to win the National Science Foundation's Alan T. Waterman Award.
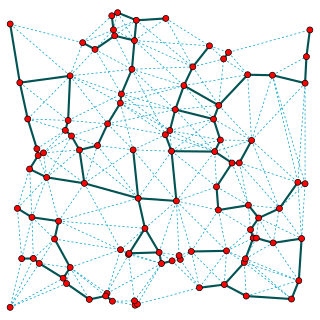
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
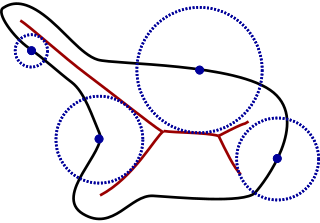
Local feature size refers to several related concepts in computer graphics and computational geometry for measuring the size of a geometric object near a particular point.
In computational geometry, a constrained Delaunay triangulation is a generalization of the Delaunay triangulation that forces certain required segments into the triangulation as edges, unlike the Delaunay triangulation itself which is based purely on the position of a given set of vertices without regard to how they should be connected by edges. It can be computed efficiently and has applications in geographic information systems and in mesh generation.
FEATool Multiphysics is a physics, finite element analysis (FEA), and partial differential equation (PDE) simulation toolbox. FEATool Multiphysics features the ability to model fully coupled heat transfer, fluid dynamics, chemical engineering, structural mechanics, fluid-structure interaction (FSI), electromagnetics, as well as user-defined and custom PDE problems in 1D, 2D (axisymmetry), or 3D, all within a graphical user interface (GUI) or optionally as script files. FEATool has been employed and used in academic research, teaching, and industrial engineering simulation contexts.
Newest Vertex Bisection is an algorithmic method to locally refine triangulations. It is widely used in computational science, numerical simulation, and computer graphics. The advantage of newest vertex bisection is that it allows local refinement of triangulations without degenerating the shape of the triangles after repeated usage.