In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.
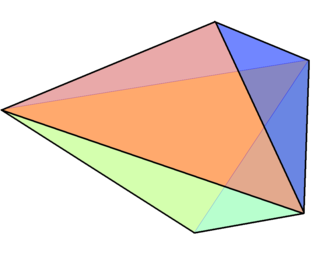
In geometry, the triangular bipyramid is the hexahedron with six triangular faces, constructed by attaching two tetrahedra face-to-face. The same shape is also called the triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of triangular bipyramid are equilateral. It is an example of a deltahedron, composite polyhedron, and Johnson solid.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid.

In 3D computer graphics, polygonal modeling is an approach for modeling objects by representing or approximating their surfaces using polygon meshes. Polygonal modeling is well suited to scanline rendering and is therefore the method of choice for real-time computer graphics. Alternate methods of representing 3D objects include NURBS surfaces, subdivision surfaces, and equation-based representations used in ray tracers.

In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

In electrical engineering and computer science, Lloyd's algorithm, also known as Voronoi iteration or relaxation, is an algorithm named after Stuart P. Lloyd for finding evenly spaced sets of points in subsets of Euclidean spaces and partitions of these subsets into well-shaped and uniformly sized convex cells. Like the closely related k-means clustering algorithm, it repeatedly finds the centroid of each set in the partition and then re-partitions the input according to which of these centroids is closest. In this setting, the mean operation is an integral over a region of space, and the nearest centroid operation results in Voronoi diagrams.

In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.

A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes. Its opposite is irregular grid.

An unstructured grid or irregular grid is a tessellation of a part of the Euclidean plane or Euclidean space by simple shapes, such as triangles or tetrahedra, in an irregular pattern. Grids of this type may be used in finite element analysis when the input to be analyzed has an irregular shape.

The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.
hp-FEM is a generalization of the finite element method (FEM) for solving partial differential equations numerically based on piecewise-polynomial approximations. hp-FEM originates from the discovery by Barna A. Szabó and Ivo Babuška that the finite element method converges exponentially fast when the mesh is refined using a suitable combination of h-refinements and p-refinements .The exponential convergence of hp-FEM has been observed by numerous independent researchers.
Smoothed finite element methods (S-FEM) are a particular class of numerical simulation algorithms for the simulation of physical phenomena. It was developed by combining meshfree methods with the finite element method. S-FEM are applicable to solid mechanics as well as fluid dynamics problems, although so far they have mainly been applied to the former.
Additive manufacturing file format (AMF) is an open standard for describing objects for additive manufacturing processes such as 3D printing. The official ISO/ASTM 52915:2016 standard is an XML-based format designed to allow any computer-aided design software to describe the shape and composition of any 3D object to be fabricated on any 3D printer via a computer-aided manufacturing software. Unlike its predecessor STL format, AMF has native support for color, materials, lattices, and constellations.
In applied mathematics, a grid or mesh is defined as the set of smaller shapes formed after discretisation of a geometric domain. Meshing has applications in the fields of geography, designing, computational fluid dynamics, and more generally in partial differential equations numerical solving. The geometric domain can be in any dimension. The two-dimensional meshing includes simple polygon, polygon with holes, multiple domain and curved domain. In three dimensions there are three types of inputs. They are simple polyhedron, geometrical polyhedron and multiple polyhedrons. Before defining the mesh type it is necessary to understand elements.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte, states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

In geometry, the ten-of-diamonds decahedron is a space-filling polyhedron with 10 faces, 2 opposite rhombi with orthogonal major axes, connected by 8 identical isosceles triangle faces. Although it is convex, it is not a Johnson solid because its faces are not composed entirely of regular polygons. Michael Goldberg named it after a playing card, as a 10-faced polyhedron with two opposite rhombic (diamond-shaped) faces. He catalogued it in a 1982 paper as 10-II, the second in a list of 26 known space-filling decahedra.
JMesh is a JSON-based portable and extensible file format for the storage and interchange of unstructured geometric data, including discretized geometries such as triangular and tetrahedral meshes, parametric geometries such as NURBS curves and surfaces, and constructive geometries such as constructive solid geometry (CGS) of shape primitives and meshes. Built upon the JData specification, a JMesh file utilizes the JSON and Universal Binary JSON (UBJSON) constructs to serialize and encode geometric data structures, therefore, it can be directly processed by most existing JSON and UBJSON parsers. The JMesh specification defines a list of JSON-compatible constructs to encode geometric data, including N-dimensional (ND) vertices, curves, surfaces, solid elements, shape primitives, their interactions and spatial relations, together with their associated properties, such as numerical values, colors, normals, materials, textures and other properties related to graphics data manipulation, 3D fabrication, computer graphics rendering and animations.
























