In number theory, an arithmetic, arithmetical, or number-theoretic function is for most authors any function f(n) whose domain is the positive integers and whose range is a subset of the complex numbers. Hardy & Wright include in their definition the requirement that an arithmetical function "expresses some arithmetical property of n".

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as
In probability theory, the central limit theorem (CLT) establishes that, in many situations, for identically distributed independent samples, the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed.
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which it is initially defined becomes divergent.
The Liouville Lambda function, denoted by λ(n) and named after Joseph Liouville, is an important arithmetic function. Its value is +1 if n is the product of an even number of prime numbers, and −1 if it is the product of an odd number of primes.
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.
In probability theory and statistics, a Gaussian process is a stochastic process, such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space.
In mathematics, a Dirichlet series is any series of the form

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.
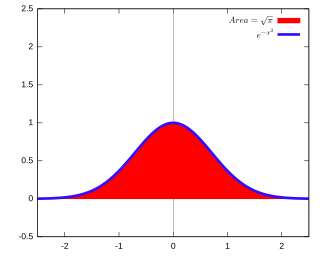
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is

In mathematics, a series expansion is a technique that expresses a function as an infinite sum, or series, of simpler functions. It is a method for calculating a function that cannot be expressed by just elementary operators.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.
Differential entropy is a concept in information theory that began as an attempt by Claude Shannon to extend the idea of (Shannon) entropy, a measure of average surprisal of a random variable, to continuous probability distributions. Unfortunately, Shannon did not derive this formula, and rather just assumed it was the correct continuous analogue of discrete entropy, but it is not. The actual continuous version of discrete entropy is the limiting density of discrete points (LDDP). Differential entropy is commonly encountered in the literature, but it is a limiting case of the LDDP, and one that loses its fundamental association with discrete entropy.
In mathematics, and more particularly in analytic number theory, Perron's formula is a formula due to Oskar Perron to calculate the sum of an arithmetic function, by means of an inverse Mellin transform.
In mathematics, Fejér's theorem, named after Hungarian mathematician Lipót Fejér, states the following:
In number theory, an average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".
In the field of mathematical analysis, a general Dirichlet series is an infinite series that takes the form of

In mathematical analysis, the Dirichlet kernel, named after the German mathematician Peter Gustav Lejeune Dirichlet, is the collection of periodic functions defined as

In probability theory, a logit-normal distribution is a probability distribution of a random variable whose logit has a normal distribution. If Y is a random variable with a normal distribution, and t is the standard logistic function, then X = t(Y) has a logit-normal distribution; likewise, if X is logit-normally distributed, then Y = logit(X)= log (X/(1-X)) is normally distributed. It is also known as the logistic normal distribution, which often refers to a multinomial logit version (e.g.).








































































