Dot planimeter

Last updated
A radius-5 circle overlaid with a grid of dots in the pattern of a dot planimeter. When counting dots near the boundary of the shape as 1/2, there are 69 interior dots and 20 boundary dots for an estimated area of 79, close to the actual area of 25p [?] 78.54. Grid points in radius-5 circle.svg
A radius-5 circle overlaid with a grid of dots in the pattern of a dot planimeter. When counting dots near the boundary of the shape as 1/2, there are 69 interior dots and 20 boundary dots for an estimated area of 79, close to the actual area of 25π ≈ 78.54.

A dot planimeter is a device used in planimetrics for estimating the area of a shape, consisting of a transparent sheet containing a square grid of dots. To estimate the area of a shape, the sheet is overlaid on the shape and the dots within the shape are counted. The estimate of area is the number of dots counted multiplied by the area of a single grid square. In some variations, dots that land on or near the boundary of the shape are counted as half of a unit. The dots may also be grouped into larger square groups by lines drawn onto the transparency, allowing groups that are entirely within the shape to be added to the count rather than requiring their dots to be counted one by one. [1]

Contents

The estimation of area by means of a dot grid has also been called the dot grid method or (particularly when the alignment of the grid with the shape is random) systematic sampling. [2] Perhaps because of its simplicity, it has been repeatedly reinvented. [3] [4] [5]

Application

In forestry, cartography, and geography, the dot planimeter has been applied to maps to estimate the area of parcels of land. [1] [4] [5] [6] In botany and horticulture, it has been applied directly to sampled leaves to estimate the average leaf area. [7] [8] [9]

In medicine, it has been applied to Lashley diagrams as an estimate of the size of brain lesions. [10]

In mineralogy, a similar technique of counting dots in a grid is applied to cross-sections of rock samples for a different purpose, estimating the relative proportions of different constituent minerals. [11]

Theory

Greater accuracy can be achieved by using a dot planimeter with a finer grid of dots. [6] Alternatively, repeatedly placing a dot planimeter with different irrational offsets from its previous placement, and averaging the resulting measurements, can lead to a set of sampled measurements whose average tends towards the true area of the measured shape. [3] The method using a finer grid tends to have better statistical efficiency than repeated measurement with random placements. [2]

According to Pick's theorem, published by Georg Alexander Pick in 1899, the version of the dot planimeter with boundary dots counting as 1/2 (and with an added correction term of −1) gives exact results for polygons that have the dots as their vertices. [12] [13] According to Blichfeldt's theorem, published by Hans Frederick Blichfeldt in 1914, it is always possible to shift a dot planimeter relative to a given shape without rotating it so that the number of dots within the shape is at least equal to its area. [14] [15]

The Gauss circle problem concerns the error that would be obtained by using a dot planimeter to estimate the area of a circle. As its name suggests, it was studied in the early 19th century by Carl Friedrich Gauss. The maximum error is known to be bounded by a fractional power of the radius of the circle, with exponent between 1/2 and 131/208. [16]

The dot planimeter differs from other types of planimeter, which measure the area of a shape by passing a device around its boundary. [5]

The Steinhaus longimeter is a similar transparency-based device for estimating the length of curves by counting crossings. [17]

Related Research Articles

Area Size of a two-dimensional surface

Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid.

Differential geometry Branch of mathematics dealing with functions and geometric structures on differentiable manifolds

Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.

History of geometry Historical development of geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).

Mathematics Field of study

Mathematics is an area of knowledge that includes such topics as numbers, formulas and related structures (algebra), shapes and the spaces in which they are contained (geometry), and quantities and their changes.

Statistics Study of the collection, analysis, interpretation, and presentation of data

Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional, to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.

Least squares Approximation method in statistics

The method of least squares is a standard approach in regression analysis to approximate the solution of overdetermined systems by minimizing the sum of the squares of the residuals made in the results of each individual equation.

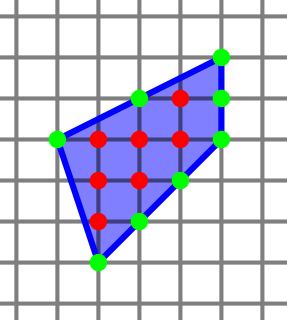
Picks theorem Formula for area of a grid polygon

In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points within it and on its boundary. The result was first described by Georg Alexander Pick in 1899. It was popularized in English by Hugo Steinhaus in the 1950 edition of his book Mathematical Snapshots. It has multiple proofs, and can be generalized to formulas for certain kinds of non-simple polygons.

A planimeter, also known as a platometer, is a measuring instrument used to determine the area of an arbitrary two-dimensional shape.

Richard Schoen American mathematician

Richard Melvin Schoen is an American mathematician known for his work in differential geometry and geometric analysis. He is best known for the resolution of the Yamabe problem in 1984.

Compressed sensing is a signal processing technique for efficiently acquiring and reconstructing a signal, by finding solutions to underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals.

Stereology is the three-dimensional interpretation of two-dimensional cross sections of materials or tissues. It provides practical techniques for extracting quantitative information about a three-dimensional material from measurements made on two-dimensional planar sections of the material. Stereology is a method that utilizes random, systematic sampling to provide unbiased and quantitative data. It is an important and efficient tool in many applications of microscopy. Stereology is a developing science with many important innovations being developed mainly in Europe. New innovations such as the proportionator continue to make important improvements in the efficiency of stereological procedures.

Steinhaus longimeter

The Steinhaus longimeter, patented by the professor Hugo Steinhaus, is an instrument used to measure the lengths of curves on maps.

Gauss circle problem How many integer lattice points there are in a circle

In mathematics, the Gauss circle problem is the problem of determining how many integer lattice points there are in a circle centered at the origin and with radius . This number is approximated by the area of the circle, so the real problem is to accurately bound the error term describing how the number of points differs from the area. The first progress on a solution was made by Carl Friedrich Gauss, hence its name.

Theil–Sen estimator Statistical method for fitting a line

In non-parametric statistics, the Theil–Sen estimator is a method for robustly fitting a line to sample points in the plane by choosing the median of the slopes of all lines through pairs of points. It has also been called Sen's slope estimator, slope selection, the single median method, the Kendall robust line-fit method, and the Kendall–Theil robust line. It is named after Henri Theil and Pranab K. Sen, who published papers on this method in 1950 and 1968 respectively, and after Maurice Kendall because of its relation to the Kendall tau rank correlation coefficient.

Hans Frederick Blichfeldt Danish-American mathematician

Hans Frederick Blichfeldt (1873–1945) was a Danish-American mathematician at Stanford University, known for his contributions to group theory, the representation theory of finite groups, the geometry of numbers, sphere packing, and quadratic forms. He is the namesake of Blichfeldt's theorem.

The Geometry of Numbers is a book on the geometry of numbers, an area of mathematics in which the geometry of lattices, repeating sets of points in the plane or higher dimensions, is used to derive results in number theory. It was written by Carl D. Olds, Anneli Cahn Lax, and Giuliana Davidoff, and published by the Mathematical Association of America in 2000 as volume 41 of their Anneli Lax New Mathematical Library book series.

Blichfeldts theorem High-area shapes can shift to hold many grid points

Blichfeldt's theorem is a mathematical theorem in the geometry of numbers, stating that whenever a bounded set in the Euclidean plane has area , it can be translated so that it includes at least points of the integer lattice. Equivalently, every bounded set of area contains a set of points whose coordinates all differ by integers.

References

  1. 1 2 Crommer, D. A. N. (January 1949), "Extracting small irregular areas", Australian Forestry, 13 (1): 64–66, doi:10.1080/00049158.1949.10675768
  2. 1 2 Bellhouse, D. R. (1981), "Area estimation by point-counting techniques", Biometrics, 37 (2): 303–312, doi:10.2307/2530419, JSTOR   2530419, MR   0673040
  3. 1 2 Steinhaus, Hugo (1924), "O mierzeniu pól płaskich" (PDF), Przegląd Matematyczno-Fizyczny (in Polish), 2 (1–2): 24–29
  4. 1 2 Abell, C. A. (1939), "A method of estimating area in irregularly shaped and broken figures" (PDF), Journal of Forestry, 37: 344–345
  5. 1 2 3 Wood, Walter F. (January 1954), "The dot planimeter, a new way to measure map area", The Professional Geographer, 6 (1): 12–14, doi:10.1111/j.0033-0124.1954.61_12.x
  6. 1 2 Frolov, Y. S.; Maling, D. H. (June 1969), "The accuracy of area measurement by point counting techniques", The Cartographic Journal, 6 (1): 21–35, doi:10.1179/caj.1969.6.1.21
  7. ↑ Heinicke, Don R. (October 1963), "Note on estimation of leaf area and leaf distribution in fruit trees", Canadian Journal of Plant Science, Canadian Science Publishing, 43 (4): 597–598, doi:10.4141/cjps63-117
  8. ↑ Benjamin, D. M.; Freeman, G. H.; Brown, E. S. (February 1968), "The determination of irregularly-shaped areas of leaves destroyed by chewing insects", Annals of Applied Biology, 61 (1): 13–17, doi:10.1111/j.1744-7348.1968.tb04505.x
  9. ↑ Dolph, Gary E. (July–September 1977), "The effect of different calculational techniques on the estimation of leaf area and the construction of leaf size distributions", Bulletin of the Torrey Botanical Club, 104 (3): 264–269, doi:10.2307/2484308, JSTOR   2484308
  10. ↑ Thomas, Roger K.; Peacock, L. J. (January 1965), "A method of measuring brain lesions", Psychonomic Science, 3 (1–12): 184, doi: 10.3758/bf03343085
  11. ↑ Neilson, M. J.; Brockman, G. F. (December 1977), "The error associated with point-counting", American Mineralogist, 62 (11–12): 1238–1244
  12. ↑ Pick, Georg (1899), "Geometrisches zur Zahlenlehre", Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen "Lotos" in Prag, (Neue Folge) (in German), 19: 311–319, JFM   33.0216.01 CiteBank:47270
  13. ↑ Wells, David (1991), "Pick's theorem", The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, pp. 183–184
  14. ↑ Blichfeldt, H. F. (1914), "A new principle in the geometry of numbers, with some applications", Transactions of the American Mathematical Society , 15 (3): 227–235, doi: 10.1090/S0002-9947-1914-1500976-6 , JSTOR   1988585, MR   1500976
  15. ↑ Olds, C. D.; Lax, Anneli; Davidoff, Giuliana P. (2000), "Chapter 9: A new principle in the geometry of numbers", The Geometry of Numbers, Anneli Lax New Mathematical Library, vol. 41, Mathematical Association of America, Washington, DC, pp. 119–127, ISBN   0-88385-643-3, MR   1817689
  16. ↑ Guy, Richard K. (2004), "F1: Gauß's lattice point problem", Unsolved Problems in Number Theory, Problem Books in Mathematics, vol. 1 (3rd ed.), New York: Springer-Verlag, pp. 365–367, doi:10.1007/978-0-387-26677-0, ISBN   0-387-20860-7, MR   2076335
  17. ↑ Steinhaus, Hugo (1931), "Longimetr", Czasopismo Geograficzne (in Polish), 3: 1–4
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.