
A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.
In Einstein's theory of general relativity, the Schwarzschild metric is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916.

The Rutherford scattering experiments were a landmark series of experiments by which scientists learned that every atom has a nucleus where all of its positive charge and most of its mass is concentrated. They deduced this after measuring how an alpha particle beam is scattered when it strikes a thin metal foil. The experiments were performed between 1906 and 1913 by Hans Geiger and Ernest Marsden under the direction of Ernest Rutherford at the Physical Laboratories of the University of Manchester.
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.

An Einstein ring, also known as an Einstein–Chwolson ring or Chwolson ring, is created when light from a galaxy or star passes by a massive object en route to the Earth. Due to gravitational lensing, the light is diverted, making it seem to come from different places. If source, lens, and observer are all in perfect alignment (syzygy), the light appears as a ring.
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric.

In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.
In general relativity, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the validation of Einstein's theory of general relativity. For example, they provide accurate predictions of the anomalous precession of the planets in the Solar System and of the deflection of light by gravity.
The Kerr–Newman metric describes the spacetime geometry around a mass which is electrically charged and rotating. It is a vacuum solution which generalizes the Kerr metric by additionally taking into account the energy of an electromagnetic field, making it the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity. As an electrovacuum solution, it only includes those charges associated with the magnetic field; it does not include any free electric charges.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

Gravitational microlensing is an astronomical phenomenon caused by the gravitational lens effect. It can be used to detect objects that range from the mass of a planet to the mass of a star, regardless of the light they emit. Typically, astronomers can only detect bright objects that emit much light (stars) or large objects that block background light. These objects make up only a minor portion of the mass of a galaxy. Microlensing allows the study of objects that emit little or no light.
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body. This theorem has particular application to astronomy.

In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion. Newton applied his theorem to understanding the overall rotation of orbits that is observed for the Moon and planets. The term "radial motion" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.
Frame-dragging is an effect on spacetime, predicted by Albert Einstein's general theory of relativity, that is due to non-static stationary distributions of mass–energy. A stationary field is one that is in a steady state, but the masses causing that field may be non-static — rotating, for instance. More generally, the subject that deals with the effects caused by mass–energy currents is known as gravitoelectromagnetism, which is analogous to the magnetism of classical electromagnetism.
The Virbhadra-Ellis lens equation in astronomy and mathematics relates to the angular positions of an unlensed source , the image , the Einstein bending angle of light , and the angular diameter lens-source and observer-source distances.
An embedded lens is a gravitational lens that consists of a concentration of mass enclosed by a relative void in the surrounding distribution of matter: both the mass and the presence of a void surrounding it will affect the path of light passing through the vicinity. This is in contrast with the simpler, more familiar gravitational lens effect, in which there is no surrounding void. While any shape and arrangement of increased and decreased mass densities will cause gravitational lensing, an ideal embedded lens would be spherical and have an internal mass density matching that of the surrounding region of space. The gravitational influence of an embedded lens differs from that of a simple gravitational lens: light rays will be bent by different angles and embedded lenses of a cosmologically significant scale would affect the spatial evolution (expansion) of the universe.
In Einstein's theory of general relativity, the interior Schwarzschild metric is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric.
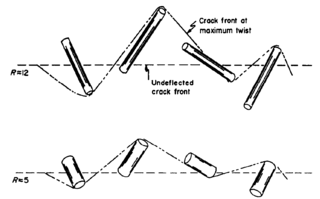
The Faber–Evans model for crack deflection, is a fracture mechanics-based approach to predict the increase in toughness in two-phase ceramic materials due to crack deflection. The effect is named after Katherine Faber and her mentor, Anthony G. Evans, who introduced the model in 1983. The Faber–Evans model is a principal strategy for tempering brittleness and creating effective ductility.




















