
In physics, Kaluza–Klein theory is a classical unified field theory of gravitation and electromagnetism built around the idea of a fifth dimension beyond the common 4D of space and time and considered an important precursor to string theory. In their setup, the vacuum has the usual 3 dimensions of space and one dimension of time but with another microscopic extra spatial dimension in the shape of a tiny circle. Gunnar Nordström had an earlier, similar idea. But in that case, a fifth component was added to the electromagnetic vector potential, representing the Newtonian gravitational potential, and writing the Maxwell equations in five dimensions.
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.
In mathematics, the Kronecker delta is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
In the general theory of relativity, the Einstein field equations relate the geometry of spacetime to the distribution of matter within it.
Semiclassical gravity is an approximation to the theory of quantum gravity in which one treats matter and energy fields as being quantum and the gravitational field as being classical.
In differential geometry, the Einstein tensor is used to express the curvature of a pseudo-Riemannian manifold. In general relativity, it occurs in the Einstein field equations for gravitation that describe spacetime curvature in a manner that is consistent with conservation of energy and momentum.
When studying and formulating Albert Einstein's theory of general relativity, various mathematical structures and techniques are utilized. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.
General relativity is a theory of gravitation that was developed by Albert Einstein between 1907 and 1915, with contributions by many others after 1915. According to general relativity, the observed gravitational attraction between masses results from the warping of space and time by those masses.
Solutions of the Einstein field equations are metrics of spacetimes that result from solving the Einstein field equations (EFE) of general relativity. Solving the field equations gives a Lorentz manifold. Solutions are broadly classed as exact or non-exact.
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational forces is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic.
In theoretical physics, massive gravity is a theory of gravity that modifies general relativity by endowing the graviton with a nonzero mass. In the classical theory, this means that gravitational waves obey a massive wave equation and hence travel at speeds below the speed of light.
Scalar theories of gravitation are field theories of gravitation in which the gravitational field is described using a scalar field, which is required to satisfy some field equation.
In the theory of general relativity, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor that incorporates the energy–momentum of gravity. It allows the energy–momentum of a system of gravitating matter to be defined. In particular it allows the total of matter plus the gravitating energy–momentum to form a conserved current within the framework of general relativity, so that the total energy–momentum crossing the hypersurface of any compact space–time hypervolume vanishes.

Robert Berks was an American sculptor, industrial designer and planner. He created hundreds of bronze sculptures and monuments including the Mary McLeod Bethune Memorial, and the Albert Einstein Memorial in Washington, D.C. Bob was prolific and created numerous sketches, drawings, and paintings; often in service of sculpture and site-planning subjects. He worked for over 50 years in a converted schoolhouse on the north fork of Long Island, NY. For projects with living subjects, Bob would often invite individuals to visit with he and Tod for a period of a week or two so he could observe them in real life; through this time he captured emotions, tendencies, facial expressions, and body language. It was this commitment to understanding his subject below the surface that facilitated the intimacy and personality found in his sculptural portraits. Bob's work is spread around the world, but he is best known for his commissions in Washington DC. Bob is one of the only artists in the world to have multiple pieces regularly on display in the Oval office. Depending on the desires of the sitting US President, Berks' busts of famed civil servants and civil rights leaders line the walls of the Oval ; most often on view are busts of FDR, Lincoln, RFK, Ronald Reagan, and JFK.
Alternatives to general relativity are physical theories that attempt to describe the phenomenon of gravitation in competition with Einstein's theory of general relativity. There have been many different attempts at constructing an ideal theory of gravity.
In mathematical physics, the Dirac algebra is the Clifford algebra . This was introduced by the mathematical physicist P. A. M. Dirac in 1928 in developing the Dirac equation for spin-1/2 particles with a matrix representation of the gamma matrices, which represent the generators of the algebra.
The Lagrangian in scalar-tensor theory can be expressed in the Jordan frame or in the Einstein frame, which are field variables that stress different aspects of the gravitational field equations and the evolution equations of the matter fields. In the Jordan frame the scalar field or some function of it multiplies the Ricci scalar in the Lagrangian and the matter is typically coupled minimally to the metric, whereas in the Einstein frame the Ricci scalar is not multiplied by the scalar field and the matter is coupled non-minimally. As a result, in the Einstein frame the field equations for the space-time metric resemble the Einstein equations but test particles do not move on geodesics of the metric. On the other hand, in the Jordan frame test particles move on geodesics, but the field equations are very different from Einstein equations. The causal structure in both frames is always equivalent and the frames can be transformed into each other as convenient for the given application.
f(R) is a type of modified gravity theory which generalizes Einstein's general relativity. f(R) gravity is actually a family of theories, each one defined by a different function, f, of the Ricci scalar, R. The simplest case is just the function being equal to the scalar; this is general relativity. As a consequence of introducing an arbitrary function, there may be freedom to explain the accelerated expansion and structure formation of the Universe without adding unknown forms of dark energy or dark matter. Some functional forms may be inspired by corrections arising from a quantum theory of gravity. f(R) gravity was first proposed in 1970 by Hans Adolph Buchdahl. It has become an active field of research following work by Starobinsky on cosmic inflation. A wide range of phenomena can be produced from this theory by adopting different functions; however, many functional forms can now be ruled out on observational grounds, or because of pathological theoretical problems.

Alexandru Proca was a Romanian physicist who studied and worked in France. He developed the vector meson theory of nuclear forces and the relativistic quantum field equations that bear his name for the massive, vector spin-1 mesons.
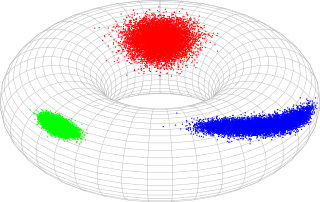
In probability theory and statistics, the bivariate von Mises distribution is a probability distribution describing values on a torus. It may be thought of as an analogue on the torus of the bivariate normal distribution. The distribution belongs to the field of directional statistics. The general bivariate von Mises distribution was first proposed by Kanti Mardia in 1975. One of its variants is today used in the field of bioinformatics to formulate a probabilistic model of protein structure in atomic detail, such as backbone-dependent rotamer libraries.










