Equitable coloring

Last updated November 21, 2023

In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that

That is, the partition of vertices among the different colors is as uniform as possible. For instance, giving each vertex a distinct color would be equitable, but would typically use many more colors than are necessary in an optimal equitable coloring. An equivalent way of defining an equitable coloring is that it is an embedding of the given graph as a subgraph of a Turán graph with the same set of vertices. There are two kinds of chromatic number associated with equitable coloring.^[1] The equitable chromatic number of a graph G is the smallest number k such that G has an equitable coloring with k colors. But G might not have equitable colorings for some larger numbers of colors; the equitable chromatic threshold of G is the smallest k such that G has equitable colorings for any number of colors greater than or equal to k.^[2]

The Hajnal–Szemerédi theorem, posed as a conjecture by PaulErdős ( 1964 ) and proven by AndrásHajnal and Endre Szemerédi ( 1970 ), states that any graph with maximum degree Δ has an equitable coloring with Δ + 1 colors. Several related conjectures remain open. Polynomial time algorithms are also known for finding a coloring matching this bound,^[3] and for finding optimal colorings of special classes of graphs, but the more general problem of deciding whether an arbitrary graph has an equitable coloring with a given number of colors is NP-complete.

Examples

An equitable coloring of the star K1,5. Equitable-K15.svg — An equitable coloring of the star K_1,5.

The star K_1,5 shown in the illustration is a complete bipartite graph, and therefore may be colored with two colors. However, the resulting coloring has one vertex in one color class and five in another, and is therefore not equitable. The smallest number of colors in an equitable coloring of this graph is four, as shown in the illustration: the central vertex must be the only vertex in its color class, so the other five vertices must be split among at least three color classes in order to ensure that the other color classes all have at most two vertices. More generally, Meyer (1973) observes that any star K_1,n needs $\scriptstyle 1+\lceil n/2\rceil$ colors in any equitable coloring; thus, the chromatic number of a graph may differ from its equitable coloring number by a factor as large as n/4. Because K_1,5 has maximum degree five, the number of colors guaranteed for it by the Hajnal–Szemerédi theorem is six, achieved by giving each vertex a distinct color.

Another interesting phenomenon is exhibited by a different complete bipartite graph, K_{2n + 1,2n + 1}. This graph has an equitable 2-coloring, given by its bipartition. However, it does not have an equitable (2n + 1)-coloring: any equitable partition of the vertices into that many color classes would have to have exactly two vertices per class, but the two sides of the bipartition cannot each be partitioned into pairs because they have an odd number of vertices. Therefore, the equitable chromatic threshold of this graph is 2n + 2, significantly greater than its equitable chromatic number of two.

Hajnal–Szemerédi theorem

Brooks' theorem states that any connected graph with maximum degree Δ has a Δ-coloring, with two exceptions (complete graphs and odd cycles). However, this coloring may in general be far from equitable. PaulErdős ( 1964 ) conjectured that an equitable coloring is possible with only one more color: any graph with maximum degree Δ has an equitable coloring with Δ + 1 colors. The case Δ = 2 is straightforward (any union of paths and cycles may be equitably colored by using a repeated pattern of three colors, with minor adjustments to the repetition when closing a cycle) and the case Δ + 1= n/3 had previously been solved by Corrádi & Hajnal (1963). The full conjecture was proven by Hajnal & Szemerédi (1970), and is now known as the Hajnal–Szemerédi theorem. Their original proof was long and complicated; a simpler proof was given by Kierstead & Kostochka (2008). A polynomial time algorithm for finding equitable colorings with this many colors was described by Kierstead and Kostochka; they credit Marcelo Mydlarz and Endre Szemerédi with a prior unpublished polynomial time algorithm. Kierstead and Kostochka also announce but do not prove a strengthening of the theorem, to show that an equitable k+1-coloring exists whenever every two adjacent vertices have degrees adding to at most 2k + 1.

Meyer (1973) conjectured a form of Brooks' theorem for equitable coloring: every connected graph with maximum degree Δ has an equitable coloring with Δ or fewer colors, with the exceptions of complete graphs and odd cycles. A strengthened version of the conjecture states that each such graph has an equitable coloring with exactly Δ colors, with one additional exception, a complete bipartite graph in which both sides of the bipartition have the same odd number of vertices.^[1]

Seymour (1974) proposed a strengthening of the Hajnal–Szemerédi theorem that also subsumes Dirac's theorem that dense graphs are Hamiltonian: he conjectured that, if every vertex in an n-vertex graph has at least kn/(k + 1) neighbors, then the graph contains as a subgraph the graph formed by connecting vertices that are at most k steps apart in an n-cycle. The case k = 1 is Dirac's theorem itself. The Hajnal–Szemerédi theorem may be recovered from this conjecture by applying the conjecture for larger values of k to the complement graph of a given graph, and using as color classes contiguous subsequences of vertices from the n-cycle. Seymour's conjecture has been approximately proven, i.e. for graphs where every vertex has at least kn/(k + 1)+o(n) neighbors.^[4] The proof uses several deep tools including the Hajnal–Szemerédi theorem itself.

Yet another generalization of the Hajnal–Szemerédi theorem is the Bollobás–Eldridge–Catlin conjecture (or BEC-conjecture for short).^[5] This states that if G₁ and G₂ are graphs on n vertices with maximum degree Δ₁ and Δ₂ respectively, and if (Δ₁ + 1)(Δ₂ + 1) ≤ n+1, then G₁ and G₂ can be packed. That is, G₁ and G₂ can be represented on the same set of n vertices with no edges in common. The Hajnal–Szemerédi theorem is the special case of this conjecture in which G₂ is a disjoint union of cliques. Catlin (1974) provides a similar but stronger condition on Δ₁ and Δ₂ under which such a packing can be guaranteed to exist.

Special classes of graphs

For any tree with maximum degree Δ, the equitable chromatic number is at most

1+\lceil \Delta /2\rceil

^[6]

with the worst case occurring for a star. However, most trees have significantly smaller equitable chromatic number: if a tree with n vertices has Δ ≤ n/3 − O(1), then it has an equitable coloring with only three colors.^[7] Furmańczyk (2006) studies the equitable chromatic number of graph products.

Computational complexity

The problem of finding equitable colorings with as few colors as possible (below the Hajnal-Szemerédi bound) has also been studied. A straightforward reduction from graph coloring to equitable coloring may be proven by adding sufficiently many isolated vertices to a graph, showing that it is NP-complete to test whether a graph has an equitable coloring with a given number of colors (greater than two). However, the problem becomes more interesting when restricted to special classes of graphs or from the point of view of parameterized complexity. Bodlaender & Fomin (2005) showed that, given a graph G and a number c of colors, it is possible to test whether G admits an equitable c-coloring in time O(n^O(t)), where t is the treewidth of G; in particular, equitable coloring may be solved optimally in polynomial time for trees (previously known due to Chen & Lih 1994) and outerplanar graphs. A polynomial time algorithm is also known for equitable coloring of split graphs.^[8] However, Fellows et al. (2007) prove that, when the treewidth is a parameter to the algorithm, the problem is W[1]-hard. Thus, it is unlikely that there exists a polynomial time algorithm independent of this parameter, or even that the dependence on the parameter may be moved out of the exponent in the formula for the running time.

Applications

One motivation for equitable coloring suggested by Meyer (1973) concerns scheduling problems. In this application, the vertices of a graph represent a collection of tasks to be performed, and an edge connects two tasks that should not be performed at the same time. A coloring of this graph represents a partition of the tasks into subsets that may be performed simultaneously; thus, the number of colors in the coloring corresponds to the number of time steps required to perform the entire task. Due to load balancing considerations, it is desirable to perform equal or nearly-equal numbers of tasks in each time step, and this balancing is exactly what an equitable coloring achieves. Furmańczyk (2006) mentions a specific application of this type of scheduling problem, assigning university courses to time slots in a way that spreads the courses evenly among the available time slots and avoids scheduling incompatible pairs of courses at the same time as each other.

The Hajnal-Szemerédi theorem has also been used to bound the variance of sums of random variables with limited dependence (Pemmaraju 2001; Janson & Ruciński 2002). If (as in the setup for the Lovász local lemma) each variable depends on at most Δ others, an equitable coloring of the dependence graph may be used to partition the variables into independent subsets within which Chernoff bounds may be calculated, resulting in tighter overall bounds on the variance than if the partition were performed in a non-equitable way.

Notes

1 2 Furmańczyk (2006).
↑ Note that, when k is greater than the number of vertices in the graph, there nevertheless exists an equitable coloring with k colors in which all color classes have zero or one vertices in them, so every graph has an equitable chromatic threshold.
↑ Kierstead, Henry A.; Kostochka, Alexandr V.; Mydlarz, Marcelo; Szemerédi, Endre (2010-09-17). "A fast algorithm for equitable coloring". Combinatorica. 30 (2): 217–224. CiteSeerX 10.1.1.224.5588 . doi:10.1007/s00493-010-2483-5. ISSN 0209-9683. S2CID 18721867.
↑ Komlós, Sárközy & Szemerédi (1998).
↑ Bollobás & Eldridge (1978).
↑ Meyer (1973).
↑ Bollobás & Guy (1983).
↑ Chen, Ko & Lih (1996).

Related Research Articles

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, an undirected graph $H$ is called a minor of the graph $G$ if $H$ can be formed from $G$ by deleting edges, vertices and by contracting edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

Extremal graph theory is a branch of combinatorics, itself an area of mathematics, that lies at the intersection of extremal combinatorics and graph theory. In essence, extremal graph theory studies how global properties of a graph influence local substructure. Results in extremal graph theory deal with quantitative connections between various graph properties, both global and local, and problems in extremal graph theory can often be formulated as optimization problems: how big or small a parameter of a graph can be, given some constraints that the graph has to satisfy? A graph that is an optimal solution to such an optimization problem is called an extremal graph, and extremal graphs are important objects of study in extremal graph theory.

<span class="mw-page-title-main">Perfect graph</span> Graph with tight clique-coloring relation

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.

In graph theory, a uniquely colorable graph is a $k$ -chromatic graph that has only one possible (proper) $k$ -coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into $k$ independent sets and there is no way to partition them into $k - 1$ independent sets.

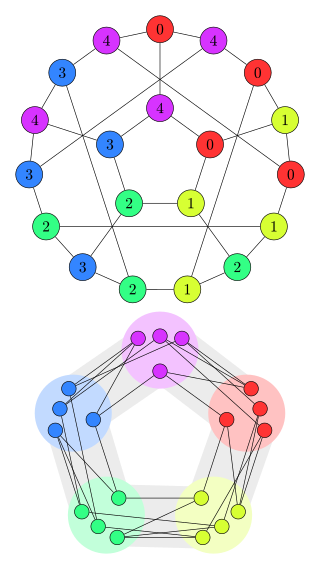
In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most $k$ different colors, for a given value of $k$ , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, a branch of mathematics, list coloring is a type of graph coloring where each vertex can be restricted to a list of allowed colors. It was first studied in the 1970s in independent papers by Vizing and by Erdős, Rubin, and Taylor.

In graph theory, the Hadwiger conjecture states that if $is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.$

In graph theory, the Hadwiger number of an undirected graph $G$ is the size of the largest complete graph that can be obtained by contracting edges of $G$ . Equivalently, the Hadwiger number $h (G)$ is the largest number $n$ for which the complete graph $K n$ is a minor of $G$ , a smaller graph obtained from $G$ by edge contractions and vertex and edge deletions. The Hadwiger number is also known as the contraction clique number of $G$ or the homomorphism degree of $G$ . It is named after Hugo Hadwiger, who introduced it in 1943 in conjunction with the Hadwiger conjecture, which states that the Hadwiger number is always at least as large as the chromatic number of $G$ .

In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree $Δ$ of the graph. At least $Δ$ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which $Δ$ colors suffice, and "class two" graphs for which $Δ + 1$ colors are necessary. A more general version of Vizing's theorem states that every undirected multigraph without loops can be colored with at most $Δ+µ$ colors, where $µ$ is the multiplicity of the multigraph. The theorem is named for Vadim G. Vizing who published it in 1964.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.

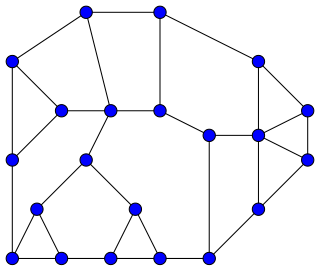
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

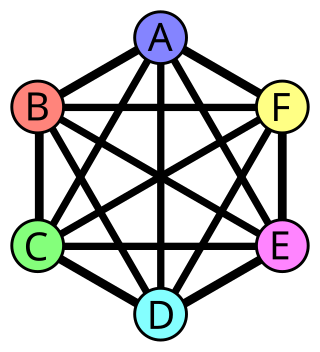
In graph theory, Brooks' theorem states a relationship between the maximum degree of a graph and its chromatic number. According to the theorem, in a connected graph in which every vertex has at most Δ neighbors, the vertices can be colored with only Δ colors, except for two cases, complete graphs and cycle graphs of odd length, which require Δ + 1 colors.

In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.

András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.

In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced subgraphs have either large cliques or large independent sets. It is named for Paul Erdős and András Hajnal.

References

Bodlaender, Hans L.; Fomin, Fedor V. (2005), "Equitable colorings of bounded treewidth graphs", Theoretical Computer Science, 349 (1): 22–30, doi: 10.1016/j.tcs.2005.09.027 , MR 2183465 .
Bollobás, B.; Eldridge, S. E. (1978), "Packings of graphs and applications to computational complexity", Journal of Combinatorial Theory , Series B, 25 (2): 105–124, doi: 10.1016/0097-3165(78)90073-0 , MR 0511983 .
Bollobás, Béla; Guy, Richard K. (1983), "Equitable and proportional coloring of trees", Journal of Combinatorial Theory , Series B, 34 (2): 177–186, doi: 10.1016/0095-8956(83)90017-5 , MR 0703602 .
Catlin, Paul A. (1974), "Subgraphs of graphs. I.", Discrete Mathematics , 10 (2): 225–233, doi: 10.1016/0012-365X(74)90119-8 , MR 0357230
Chen, Bor-Liang; Lih, Ko-Wei (1994), "Equitable coloring of trees", Journal of Combinatorial Theory , Series B, 61 (1): 83–87, doi: 10.1006/jctb.1994.1032 , MR 1275266 .
Chen, Bor-Liang; Ko, Ming-Tat; Lih, Ko-Wei (1996), "Equitable and m-bounded coloring of split graphs", Combinatorics and Computer Science (Brest, 1995), Lecture Notes in Computer Science, vol. 1120, Berlin: Springer-Verlag, pp. 1–5, doi:10.1007/3-540-61576-8_67, ISBN 978-3-540-61576-7, MR 1448914
Corrádi, K.; Hajnal, A. (1963), "On the maximal number of independent circuits in a graph", Acta Mathematica Academiae Scientiarum Hungaricae , 14 (3–4): 423–439, doi: 10.1007/BF01895727 , MR 0200185 .
Erdős, Paul (1964), "Problem 9", in Fieldler, M. (ed.), Theory of Graphs and its Applications, Prague: Czech Acad. Sci. Publ., p. 159.
Fellows, Michael; Fomin, Fedor V.; Lokshtanov, Daniel; Rosamond, Frances; Saurabh, Saket; Szeider, Stefan; Thomassen, Carsten (2007), "On the complexity of some colorful problems parameterized by treewidth", Combinatorial optimization and applications (PDF), Lecture Notes in Computer Science, vol. 4616, Berlin: Springer-Verlag, pp. 366–377, doi:10.1007/978-3-540-73556-4_38, ISBN 978-3-540-73555-7, MR 2397574, S2CID 5621950 .
Furmańczyk, Hanna (2006), "Equitable coloring of graph products" (PDF), Opuscula Mathematica , 26 (1): 31–44, MR 2272280 .
Hajnal, A.; Szemerédi, E. (1970), "Proof of a conjecture of P. Erdős", Combinatorial theory and its applications, II (Proc. Colloq., Balatonfüred, 1969), North-Holland, pp. 601–623, MR 0297607 .
Janson, Svante; Ruciński, Andrzej (2002), "The infamous upper tail", Random Structures & Algorithms, 20 (3): 317–342, doi: 10.1002/rsa.10031 , MR 1900611, S2CID 8294505 .
Kierstead, H. A.; Kostochka, A. V. (2008), "A short proof of the Hajnal-Szemerédi theorem on equitable colouring", Combinatorics, Probability and Computing , 17 (2): 265–270, doi:10.1017/S0963548307008619, MR 2396352, S2CID 12254683
Komlós, János; Sárközy, Gábor N.; Szemerédi, Endre (1998), "Proof of the Seymour conjecture for large graphs", Annals of Combinatorics , 2 (1): 43–60, CiteSeerX 10.1.1.122.2352 , doi: 10.1007/BF01626028 , MR 1682919 .
Meyer, Walter (1973), "Equitable coloring", American Mathematical Monthly , 80 (8): 920–922, doi:10.2307/2319405, JSTOR 2319405 .
Pemmaraju, Sriram V. (2001), "Equitable colorings extend Chernoff-Hoeffding bounds", Proc. 12th ACM-SIAM Symp. Discrete Algorithms (SODA 2001), Soda '01, pp. 924–925, ISBN 9780898714906 .
Seymour, P. (1974), "Problem section", in McDonough, T. P.; Mavron, Eds., V. C. (eds.), Combinatorics: Proceedings of the British Combinatorial Conference 1973, Cambridge, UK: Cambridge Univ. Press, pp. 201–202.

External links

ECOPT A Branch and Cut algorithm for solving the Equitable Coloring Problem

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[F06-1] 1 2 Furmańczyk (2006).

[2] Note that, when k is greater than the number of vertices in the graph, there nevertheless exists an equitable coloring with k colors in which all color classes have zero or one vertices in them, so every graph has an equitable chromatic threshold.

[3] Kierstead, Henry A.; Kostochka, Alexandr V.; Mydlarz, Marcelo; Szemerédi, Endre (2010-09-17). "A fast algorithm for equitable coloring". Combinatorica. 30 (2): 217–224. CiteSeerX 10.1.1.224.5588 . doi:10.1007/s00493-010-2483-5. ISSN 0209-9683. S2CID 18721867.

[4] Komlós, Sárközy & Szemerédi (1998).

[5] Bollobás & Eldridge (1978).

[6] Meyer (1973).

[7] Bollobás & Guy (1983).

[8] Chen, Ko & Lih (1996).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]