The Riesz representation theorem, sometimes called the Riesz–Fréchet representation theorem after Frigyes Riesz and Maurice René Fréchet, establishes an important connection between a Hilbert space and its continuous dual space. If the underlying field is the real numbers, the two are isometrically isomorphic; if the underlying field is the complex numbers, the two are isometrically anti-isomorphic. The (anti-) isomorphism is a particular natural isomorphism.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as or where is the Laplace operator, is the divergence operator, is the gradient operator, and is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function.

In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities used in Lagrangian mechanics with (generalized) momenta. Both theories provide interpretations of classical mechanics and describe the same physical phenomena.
In mathematics, a linear form is a linear map from a vector space to its field of scalars.

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.

The path integral formulation is a description in quantum mechanics that generalizes the stationary action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
In mathematics, an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular, often infinite, point. Investigations by Dingle (1973) revealed that the divergent part of an asymptotic expansion is latently meaningful, i.e. contains information about the exact value of the expanded function.
In probability theory and related fields, Malliavin calculus is a set of mathematical techniques and ideas that extend the mathematical field of calculus of variations from deterministic functions to stochastic processes. In particular, it allows the computation of derivatives of random variables. Malliavin calculus is also called the stochastic calculus of variations. P. Malliavin first initiated the calculus on infinite dimensional space. Then, the significant contributors such as S. Kusuoka, D. Stroock, J-M. Bismut, Shinzo Watanabe, I. Shigekawa, and so on finally completed the foundations.

In quantum field theory, the Lehmann–Symanzik–Zimmermann (LSZ) reduction formula is a method to calculate S-matrix elements from the time-ordered correlation functions of a quantum field theory. It is a step of the path that starts from the Lagrangian of some quantum field theory and leads to prediction of measurable quantities. It is named after the three German physicists Harry Lehmann, Kurt Symanzik and Wolfhart Zimmermann.
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proven difficult to formulate a precise definition of stiffness, but the main idea is that the equation includes some terms that can lead to rapid variation in the solution.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z).
In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T || ≤ 1. This notion is a special case of the concept of a contraction mapping, but every bounded operator becomes a contraction after suitable scaling. The analysis of contractions provides insight into the structure of operators, or a family of operators. The theory of contractions on Hilbert space is largely due to Béla Szőkefalvi-Nagy and Ciprian Foias.
In applied mathematics, discontinuous Galerkin methods (DG methods) form a class of numerical methods for solving differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic, parabolic and mixed form problems arising from a wide range of applications. DG methods have in particular received considerable interest for problems with a dominant first-order part, e.g. in electrodynamics, fluid mechanics and plasma physics. Indeed, the solutions of such problems may involve strong gradients (and even discontinuities) so that classical finite element methods fail, while finite volume methods are restricted to low order approximations.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix is a matrix that represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.
In mathematics, the method of steepest descent or saddle-point method is an extension of Laplace's method for approximating an integral, where one deforms a contour integral in the complex plane to pass near a stationary point, in roughly the direction of steepest descent or stationary phase. The saddle-point approximation is used with integrals in the complex plane, whereas Laplace’s method is used with real integrals.
Coherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the article Coherent states. However, they have generated a huge variety of generalizations, which have led to a tremendous amount of literature in mathematical physics. In this article, we sketch the main directions of research on this line. For further details, we refer to several existing surveys.
In mathematics, and especially algebraic geometry, a Bridgeland stability condition, defined by Tom Bridgeland, is an algebro-geometric stability condition defined on elements of a triangulated category. The case of original interest and particular importance is when this triangulated category is the derived category of coherent sheaves on a Calabi–Yau manifold, and this situation has fundamental links to string theory and the study of D-branes.
In mathematics, calculus on Euclidean space is a generalization of calculus of functions in one or several variables to calculus of functions on Euclidean space as well as a finite-dimensional real vector space. This calculus is also known as advanced calculus, especially in the United States. It is similar to multivariable calculus but is somewhat more sophisticated in that it uses linear algebra more extensively and covers some concepts from differential geometry such as differential forms and Stokes' formula in terms of differential forms. This extensive use of linear algebra also allows a natural generalization of multivariable calculus to calculus on Banach spaces or topological vector spaces.
In stochastic calculus, the Ogawa integral, also called the non-causal stochastic integral, is a stochastic integral for non-adapted processes as integrands. The corresponding calculus is called non-causal calculus in order to distinguish it from the anticipating calculus of the Skorokhod integral. The term causality refers to the adaptation to the natural filtration of the integrator.
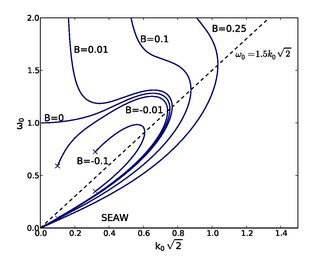
A nonlinear dispersion relation (NDR) is a dispersion relation that assigns the correct phase velocity to a nonlinear wave structure. As an example of how diverse and intricate the underlying description can be, we deal with plane electrostatic wave structures which propagate with in a collisionless plasma. Such structures are ubiquitous, for example in the magnetosphere of the Earth, in fusion reactors or in the laboratory. Correct means that this must be done according to the governing equations, in this case the Vlasov-Poisson system, and the conditions prevailing in the plasma during the wave formation process. This means that special attention must be paid to the particle trapping processes acting on the resonant electrons and ions, which requires phase space analyses. Since the latter is stochastic, transient and rather filamentary in nature, the entire dynamic trapping process eludes mathematical treatment, so that it can be adequately taken into account “only” in the asymptotic, quiet regime of wave generation, when the structure is close to equilibrium.













































































