Free particle

In physics, a free particle is a particle that, in some sense, is not bound by an external force, or equivalently not in a region where its potential energy varies. In classical physics, this means the particle is present in a "field-free" space. In quantum mechanics, it means the particle is in a region of uniform potential, usually set to zero in the region of interest since the potential can be arbitrarily set to zero at any point in space.

Classical free particle

The classical free particle is characterized by a fixed velocity v. The momentum is given by $${\displaystyle \mathbf {p} =m\mathbf {v} }$$ and the kinetic energy (equal to total energy) by $${\displaystyle E={\frac {1}{2}}mv^{2}={\frac {p^{2}}{2m}}}$$ where m is the mass of the particle and v is the vector velocity of the particle.

Quantum free particle

Propagation of de Broglie waves in 1d - real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the colour opacity) of finding the particle at a given point x is spread out like a waveform, there is no definite position of the particle. As the amplitude increases above zero the curvature decreases, so the decreases again, and vice versa - the result is an alternating amplitude: a wave. Top: Plane wave. Bottom: Wave packet.

Mathematical description

Main articles: Schrödinger equation and Matter wave

A free particle with mass ${\displaystyle m}$ in non-relativistic quantum mechanics is described by the free Schrödinger equation: $${\displaystyle -{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\ \psi (\mathbf {r} ,t)=i\hbar {\frac {\partial }{\partial t}}\psi (\mathbf {r} ,t)}$$

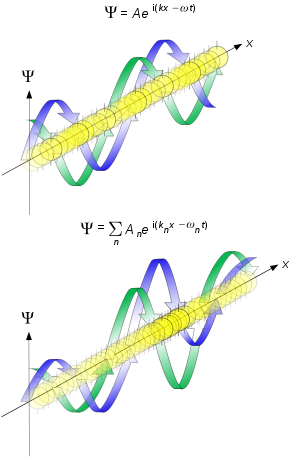
where ψ is the wavefunction of the particle at position r and time t. The solution for a particle with momentum p or wave vector k, at angular frequency ω or energy E, is given by a complex plane wave:

$${\displaystyle \psi (\mathbf {r} ,t)=Ae^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}=Ae^{i(\mathbf {p} \cdot \mathbf {r} -Et)/\hbar }}$$

with amplitude A and has two different rules according to its mass:

1. if the particle has mass ${\displaystyle m}$: ${\textstyle \omega ={\frac {\hbar k^{2}}{2m}}}$ (or equivalent ${\textstyle E={\frac {p^{2}}{2m}}}$).
2. if the particle is a massless particle: ${\displaystyle \omega =kc}$.

The eigenvalue spectrum is infinitely degenerate since for each eigenvalue E>0, there corresponds an infinite number of eigenfunctions corresponding to different directions of ${\displaystyle \mathbf {p} }$.

The De Broglie relations: ${\displaystyle \mathbf {p} =\hbar \mathbf {k} }$, ${\displaystyle E=\hbar \omega }$ apply. Since the potential energy is (stated to be) zero, the total energy E is equal to the kinetic energy, which has the same form as in classical physics:

$${\displaystyle E=T\,\rightarrow \,{\frac {\hbar ^{2}k^{2}}{2m}}=\hbar \omega }$$

As for all quantum particles free or bound, the Heisenberg uncertainty principles ${\textstyle \Delta p_{x}\Delta x\geq {\frac {\hbar }{2}}}$ apply. It is clear that since the plane wave has definite momentum (definite energy), the probability of finding the particle's location is uniform and negligible all over the space. In other words, the wave function is not normalizable in a Euclidean space, these stationary states can not correspond to physical realizable states. ^[1]

Measurement and calculations

The integral of the probability density function

$${\displaystyle \rho (\mathbf {r} ,t)=\psi ^{*}(\mathbf {r} ,t)\psi (\mathbf {r} ,t)=|\psi (\mathbf {r} ,t)|^{2}}$$

where * denotes complex conjugate, over all space is the probability of finding the particle in all space, which must be unity if the particle exists: $${\displaystyle \int _{\mathrm {all\,space} }|\psi (\mathbf {r} ,t)|^{2}d^{3}\mathbf {r} =1}$$

This is the normalization condition for the wave function. The wavefunction is not normalizable for a plane wave, but is for a wave packet.

Increasing amounts of wavepacket localization, meaning the particle becomes more localized.

In the limit ħ → 0, the particle's position and momentum become known exactly.

Interpretation of wave function for one spin-0 particle in one dimension. The wavefunctions shown are continuous, finite, single-valued and normalized. The colour opacity (%) of the particles corresponds to the probability density (which can measure in %) of finding the particle at the points on the x-axis.

Fourier decomposition

The free particle wave function may be represented by a superposition of momentum eigenfunctions, with coefficients given by the Fourier transform of the initial wavefunction: ^[2]

$${\displaystyle \psi (\mathbf {r} ,t)={\frac {1}{({\sqrt {2\pi }})^{3}}}\int _{\mathrm {all\,\mathbf {k} \,space} }{\hat {\psi }}_{0}(\mathbf {k} )e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}d^{3}\mathbf {k} }$$

where the integral is over all k-space and ${\textstyle \omega =\omega (\mathbf {k} )={\frac {\hbar \mathbf {k} ^{2}}{2m}}}$ (to ensure that the wave packet is a solution of the free particle Schrödinger equation). Here ${\displaystyle \psi _{0}}$ is the value of the wave function at time 0 and ${\displaystyle {\hat {\psi }}_{0}}$ is the Fourier transform of ${\displaystyle \psi _{0}}$. (The Fourier transform ${\displaystyle {\hat {\psi }}_{0}(\mathbf {k} )}$ is essentially the momentum wave function of the position wave function ${\displaystyle \psi _{0}(\mathbf {r} )}$, but written as a function of ${\displaystyle \mathbf {k} }$ rather than ${\displaystyle \mathbf {p} =\hbar \mathbf {k} }$.)

The expectation value of the momentum p for the complex plane wave is

$${\displaystyle \langle \mathbf {p} \rangle =\left\langle \psi \left|-i\hbar \nabla \right|\psi \right\rangle =\hbar \mathbf {k} ,}$$

and for the general wave packet it is

$${\displaystyle \langle \mathbf {p} \rangle =\int _{\mathrm {all\,space} }\psi ^{*}(\mathbf {r} ,t)(-i\hbar \nabla )\psi (\mathbf {r} ,t)d^{3}\mathbf {r} =\int _{\mathrm {all\,{\textbf {k}}\,space} }\hbar \mathbf {k} |{\hat {\psi }}_{0}(\mathbf {k} )|^{2}d^{3}\mathbf {k} .}$$

The expectation value of the energy E is

$${\displaystyle \langle E\rangle =\left\langle \psi \left|-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\right|\psi \right\rangle =\int _{\text{all space}}\psi ^{*}(\mathbf {r} ,t)\left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\right)\psi (\mathbf {r} ,t)d^{3}\mathbf {r} .}$$

Group velocity and phase velocity

Propagation of a wave packet, with the motion of a single peak shaded in purple. The peaks move at the phase velocity while the overall packet moves at the group velocity.

The phase velocity is defined to be the speed at which a plane wave solution propagates, namely

$${\displaystyle v_{p}={\frac {\omega }{k}}={\frac {\hbar k}{2m}}={\frac {p}{2m}}.}$$

Note that ${\displaystyle {\frac {p}{2m}}}$ is not the speed of a classical particle with momentum ${\displaystyle p}$; rather, it is half of the classical velocity.

Meanwhile, suppose that the initial wave function ${\displaystyle \psi _{0}}$ is a wave packet whose Fourier transform ${\displaystyle {\hat {\psi }}_{0}}$ is concentrated near a particular wave vector ${\displaystyle \mathbf {k} }$. Then the group velocity of the plane wave is defined as $${\displaystyle v_{g}=\nabla \omega (\mathbf {k} )={\frac {\hbar \mathbf {k} }{m}}={\frac {\mathbf {p} }{m}},}$$

which agrees with the formula for the classical velocity of the particle. The group velocity is the (approximate) speed at which the whole wave packet propagates, while the phase velocity is the speed at which the individual peaks in the wave packet move. ^[3] The figure illustrates this phenomenon, with the individual peaks within the wave packet propagating at half the speed of the overall packet.

Spread of the wave packet

The notion of group velocity is based on a linear approximation to the dispersion relation ${\displaystyle \omega (k)}$ near a particular value of ${\displaystyle k}$. ^[4] In this approximation, the amplitude of the wave packet moves at a velocity equal to the group velocity without changing shape. This result is an approximation that fails to capture certain interesting aspects of the evolution a free quantum particle. Notably, the width of the wave packet, as measured by the uncertainty in the position, grows linearly in time for large times. This phenomenon is called the spread of the wave packet for a free particle.

Specifically, it is not difficult to compute an exact formula for the uncertainty ${\displaystyle \Delta _{\psi (t)}X}$ as a function of time, where ${\displaystyle X}$ is the position operator. Working in one spatial dimension for simplicity, we have: ^[5] $${\displaystyle (\Delta _{\psi (t)}X)^{2}={\frac {t^{2}}{m^{2}}}(\Delta _{\psi _{0}}P)^{2}+{\frac {2t}{m}}\left(\left\langle {\tfrac {1}{2}}({XP+PX})\right\rangle _{\psi _{0}}-\left\langle X\right\rangle _{\psi _{0}}\left\langle P\right\rangle _{\psi _{0}}\right)+(\Delta _{\psi _{0}}X)^{2},}$$ where ${\displaystyle \psi _{0}}$ is the time-zero wave function. The expression in parentheses in the second term on the right-hand side is the quantum covariance of ${\displaystyle X}$ and ${\displaystyle P}$.

Thus, for large positive times, the uncertainty in ${\displaystyle X}$ grows linearly, with the coefficient of ${\displaystyle t}$ equal to ${\displaystyle (\Delta _{\psi _{0}}P)/m}$. If the momentum of the initial wave function ${\displaystyle \psi _{0}}$ is highly localized, the wave packet will spread slowly and the group-velocity approximation will remain good for a long time. Intuitively, this result says that if the initial wave function has a very sharply defined momentum, then the particle has a sharply defined velocity and will (to good approximation) propagate at this velocity for a long time.

Relativistic quantum free particle

Main article: Quantum field theory

There are a number of equations describing relativistic particles: see relativistic wave equations.

See also

• Wave packet
• Group velocity
• Particle in a box
• Finite square well
• Delta potential

References

• Quantum Mechanics, E. Abers, Pearson Ed., Addison Wesley, Prentice Hall Inc, 2004, ISBN   978-0-13-146100-0
• Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd Edition), R. Eisberg, R. Resnick, John Wiley & Sons, 1985, ISBN   978-0-471-87373-0
• Stationary States, A. Holden, College Physics Monographs (USA), Oxford University Press, 1971, ISBN   0-19-851121-3
• Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, vol. 267, Springer, Bibcode:2013qtm..book.....H, ISBN   978-1461471158
• Quantum Mechanics Demystified, D. McMahon, Mc Graw Hill (USA), 2006, ISBN   0-07-145546 9
• Elementary Quantum Mechanics, N.F. Mott, Wykeham Science, Wykeham Press (Taylor & Francis Group), 1972, ISBN   0-85109-270-5
• Quantum mechanics, E. Zaarur, Y. Peleg, R. Pnini, Schaum's Outlines, Mc Graw Hill (USA), 1998, ISBN   007-0540187

Specific

1. "Lecture 9" (PDF).
2. Hall 2013 Section 4.1
3. Hall 2013 Sections 4.3 and 4.4
4. Hall 2013 Equation 4.24
5. Hall 2013 Proposition 4.10

Further reading

• The New Quantum Universe, T.Hey, P.Walters, Cambridge University Press, 2009, ISBN   978-0-521-56457-1.
• Quantum Field Theory, D. McMahon, Mc Graw Hill (USA), 2008, ISBN   978-0-07-154382-8
• Quantum mechanics, E. Zaarur, Y. Peleg, R. Pnini, Schaum's Easy Outlines Crash Course, Mc Graw Hill (USA), 2006, ISBN   978-007-145533-6