Related Research Articles

In mathematics and computer science, an algorithm is a finite sequence of well-defined, computer-implementable instructions, typically to solve a class of specific problems or to perform a computation. Algorithms are always unambiguous and are used as specifications for performing calculations, data processing, automated reasoning, and other tasks. In contrast, a heuristic is a technique used in problem solving that uses practical methods and/or various estimates in order to produce solutions that may not be optimal but are sufficient given the circumstances.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random determined by the random bits; thus either the running time, or the output are random variables.
Trajectory optimization is the process of designing a trajectory that minimizes some measure of performance while satisfying a set of constraints. Generally speaking, trajectory optimization is a technique for computing an open-loop solution to an optimal control problem. It is often used for systems where computing the full closed-loop solution is not required, impractical or impossible. If a trajectory optimization problem can be solved at a rate given by the inverse of the Lipschitz constant, then it can be used iteratively to generate a closed-loop solution in the sense of Caratheodory. If only the first step of the trajectory is executed for an infinite-horizon problem, then this is known as Model Predictive Control (MPC).
Uncertainty quantification (UQ) is the science of quantitative characterization and reduction of uncertainties in both computational and real world applications. It tries to determine how likely certain outcomes are if some aspects of the system are not exactly known. An example would be to predict the acceleration of a human body in a head-on crash with another car: even if the speed was exactly known, small differences in the manufacturing of individual cars, how tightly every bolt has been tightened, etc., will lead to different results that can only be predicted in a statistical sense.
The polyhedral model is a mathematical framework for programs that perform large numbers of operations -- too large to be explicitly enumerated -- thereby requiring a compact representation. Nested loop programs are the typical, but not the only example, and the most common use of the model is for loop nest optimization in program optimization. The polyhedral method treats each loop iteration within nested loops as lattice points inside mathematical objects called polyhedra, performs affine transformations or more general non-affine transformations such as tiling on the polytopes, and then converts the transformed polytopes into equivalent, but optimized, loop nests through polyhedra scanning.
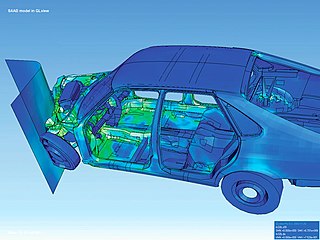
The finite element method (FEM) is a widely used method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.

In numerical analysis, the interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics, composite structures, biomechanics and in many other areas. The goal of the Interval Finite Element is to find upper and lower bounds of different characteristics of the model and use these results in the design process. This is so called worst case design, which is closely related to the limit state design.
Interval boundary element method is classical boundary element method with the interval parameters.
Boundary element method is based on the following integral equation
Z88 is a software package for the finite element method (FEM) and topology optimization. A team led by Frank Rieg at the University of Bayreuth started development in 1985 and now the software is used by several universities, as well as small and medium-sized enterprises. Z88 is capable of calculating two and three dimensional element types with a linear approach. The software package contains several solvers and two post-processors and is available for Microsoft Windows, Mac OS X and Unix/Linux computers in 32-bit and 64-bit versions. Benchmark tests conducted in 2007 showed a performance on par with commercial software.
Fitness approximation aims to approximate the objective or fitness functions in evolutionary optimization by building up machine learning models based on data collected from numerical simulations or physical experiments. The machine learning models for fitness approximation are also known as meta-models or surrogates, and evolutionary optimization based on approximated fitness evaluations are also known as surrogate-assisted evolutionary approximation. Fitness approximation in evolutionary optimization can be seen as a sub-area of data-driven evolutionary optimization.
OptiY is a design environment providing modern optimization strategies and state of the art probabilistic algorithms for uncertainty, reliability, robustness, sensitivity analysis, data-mining and meta-modeling.

StressCheck is a finite element analysis software product developed and supported by ESRD, Inc. of St. Louis, Missouri. It is one of the first commercially available FEA products to utilize the p-version of the finite element method and support verification and validation in computational solid mechanics and the requirements of Simulation Governance.
FEMtools is a multi-functional, cross-platform and solver-independent family of CAE software programs providing analysis and scripting solutions for many different types of applications. The program is developed, supported and licensed by Dynamic Design Solutions ("DDS") NV.
Optimus is a Process Integration and Design Optimization (PIDO) platform developed by Noesis Solutions. Noesis Solutions takes part in key research projects, such as MEGaFIT, JTI CleanSky Green Rotorcraft and iProd.
References
- ↑ Michael Hanss, 2005. Applied Fuzzy Arithmetic, An Introduction with Engineering Applications. Springer, ISBN 3-540-24201-5