Genus 0
An orientable surface of genus zero is the sphere S2. Another surface of genus zero is the disc.
- Representations of genus 0 surfaces
A sphere
A closed disc (with boundary)
In mathematics, a genus g surface (also known as a g-torus or g-holed torus) is a surface formed by the connected sum of g distinct tori: the interior of a disk is removed from each of g distinct tori and the boundaries of the g many disks are identified (glued together), forming a g-torus. The genus of such a surface is g.
A genus g surface is a two-dimensional manifold. The classification theorem for surfaces states that every compact connected two-dimensional manifold is homeomorphic to either the sphere, the connected sum of tori, or the connected sum of real projective planes.
The genus of a connected orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. [1] It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic χ, via the relationship χ = 2 − 2g for closed surfaces, where g is the genus.
The genus (sometimes called the demigenus or Euler genus) of a connected non-orientable closed surface is a positive integer representing the number of cross-caps attached to a sphere. Alternatively, it can be defined for a closed surface in terms of the Euler characteristic χ, via the relationship χ = 2 − g, where g is the non-orientable genus.
An orientable surface of genus zero is the sphere S2. Another surface of genus zero is the disc.
A genus one orientable surface is the ordinary torus. A non-orientable surface of genus one is the projective plane. [2]
Elliptic curves over the complex numbers can be identified with genus 1 surfaces. The formulation of elliptic curves as the embedding of a torus in the complex projective plane follows naturally from a property of Weierstrass's elliptic functions that allows elliptic curves to be obtained from the quotient of the complex plane by a lattice. [3]
The term double torus is occasionally used to denote a genus 2 surface. [4] [5] A non-orientable surface of genus two is the Klein bottle.
The Bolza surface is the most symmetric Riemann surface of genus 2, in the sense that it has the largest possible conformal automorphism group. [6]
The term triple torus is also occasionally used to denote a genus 3 surface. [7] [5]
The Klein quartic is a compact Riemann surface of genus 3 with the highest possible order automorphism group for compact Riemann surfaces of genus 3. It has 168 orientation-preserving automorphisms, and 336 automorphisms altogether.
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.
In mathematics, genus has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1.
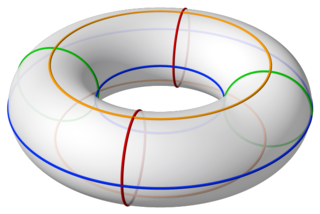
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.
In the mathematical field of differential geometry, the Gauss–Bonnet theorem is a fundamental formula which links the curvature of a surface to its underlying topology.
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by .
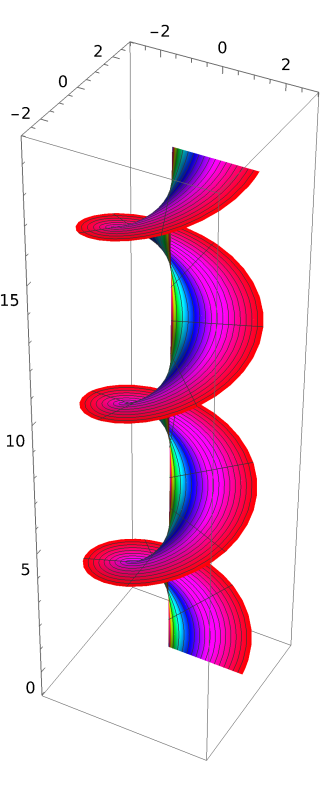
In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or several sheets glued together.
In mathematics, Thurston's geometrization conjecture states that each of certain three-dimensional topological spaces has a unique geometric structure that can be associated with it. It is an analogue of the uniformization theorem for two-dimensional surfaces, which states that every simply connected Riemann surface can be given one of three geometries . In three dimensions, it is not always possible to assign a single geometry to a whole topological space. Instead, the geometrization conjecture states that every closed 3-manifold can be decomposed in a canonical way into pieces that each have one of eight types of geometric structure. The conjecture was proposed by William Thurston, and implies several other conjectures, such as the Poincaré conjecture and Thurston's elliptization conjecture.
In mathematics, the uniformization theorem states that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generalization of the Riemann mapping theorem from simply connected open subsets of the plane to arbitrary simply connected Riemann surfaces.
In mathematics, the Riemann–Hurwitz formula, named after Bernhard Riemann and Adolf Hurwitz, describes the relationship of the Euler characteristics of two surfaces when one is a ramified covering of the other. It therefore connects ramification with algebraic topology, in this case. It is a prototype result for many others, and is often applied in the theory of Riemann surfaces and algebraic curves.
In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
A Seifert fiber space is a 3-manifold together with a decomposition as a disjoint union of circles. In other words, it is a -bundle over a 2-dimensional orbifold. Many 3-manifolds are Seifert fiber spaces, and they account for all compact oriented manifolds in 6 of the 8 Thurston geometries of the geometrization conjecture.
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.
In mathematics, specifically in symplectic topology and algebraic geometry, one can construct the moduli space of stable maps, satisfying specified conditions, from Riemann surfaces into a given symplectic manifold. This moduli space is the essence of the Gromov–Witten invariants, which find application in enumerative geometry and type IIA string theory. The idea of stable map was proposed by Maxim Kontsevich around 1992 and published in Kontsevich (1995).
In mathematics, Hopf conjecture may refer to one of several conjectural statements from differential geometry and topology attributed to Heinz Hopf.
Geometric function theory is the study of geometric properties of analytic functions. A fundamental result in the theory is the Riemann mapping theorem.
In mathematics, a Klein surface is a dianalytic manifold of complex dimension 1. Klein surfaces may have a boundary and need not be orientable. Klein surfaces generalize Riemann surfaces. While the latter are used to study algebraic curves over the complex numbers analytically, the former are used to study algebraic curves over the real numbers analytically. Klein surfaces were introduced by Felix Klein in 1882.
In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold into topological disks such that every flag can be transformed into any other flag by a symmetry of the decomposition. Regular maps are, in a sense, topological generalizations of Platonic solids. The theory of maps and their classification is related to the theory of Riemann surfaces, hyperbolic geometry, and Galois theory. Regular maps are classified according to either: the genus and orientability of the supporting surface, the underlying graph, or the automorphism group.
