Greedy embedding

Last updated

In distributed computing and geometric graph theory, greedy embedding is a process of assigning coordinates to the nodes of a telecommunications network in order to allow greedy geographic routing to be used to route messages within the network. Although greedy embedding has been proposed for use in wireless sensor networks, in which the nodes already have positions in physical space, these existing positions may differ from the positions given to them by greedy embedding, which may in some cases be points in a virtual space of a higher dimension, or in a non-Euclidean geometry. In this sense, greedy embedding may be viewed as a form of graph drawing, in which an abstract graph (the communications network) is embedded into a geometric space.

Contents

The idea of performing geographic routing using coordinates in a virtual space, instead of using physical coordinates, is due to Rao et al. [1] Subsequent developments have shown that every network has a greedy embedding with succinct vertex coordinates in the hyperbolic plane, that certain graphs including the polyhedral graphs have greedy embeddings in the Euclidean plane, and that unit disk graphs have greedy embeddings in Euclidean spaces of moderate dimensions with low stretch factors.

Definitions

In greedy routing, a message from a source node s to a destination node t travels to its destination by a sequence of steps through intermediate nodes, each of which passes the message on to a neighboring node that is closer to t. If the message reaches an intermediate node x that does not have a neighbor closer to t, then it cannot make progress and the greedy routing process fails. A greedy embedding is an embedding of the given graph with the property that a failure of this type is impossible. Thus, it can be characterized as an embedding of the graph with the property that for every two nodes x and t, there exists a neighbor y of x such that d(x,t) > d(y,t), where d denotes the distance in the embedded space. [2]

Graphs with no greedy embedding

K1,6, a graph with no greedy embedding in the Euclidean plane Sextic-monomial-dessin.svg
K1,6, a graph with no greedy embedding in the Euclidean plane

Not every graph has a greedy embedding into the Euclidean plane; a simple counterexample is given by the star K1,6, a tree with one internal node and six leaves. [2] Whenever this graph is embedded into the plane, some two of its leaves must form an angle of 60 degrees or less, from which it follows that at least one of these two leaves does not have a neighbor that is closer to the other leaf.

In Euclidean spaces of higher dimensions, more graphs may have greedy embeddings; for instance, K1,6 has a greedy embedding into three-dimensional Euclidean space, in which the internal node of the star is at the origin and the leaves are a unit distance away along each coordinate axis. However, for every Euclidean space of fixed dimension, there are graphs that cannot be embedded greedily: whenever the number n is greater than the kissing number of the space, the graph K1,n has no greedy embedding. [3]

Hyperbolic and succinct embeddings

Unlike the case for the Euclidean plane, every network has a greedy embedding into the hyperbolic plane. The original proof of this result, by Robert Kleinberg, required the node positions to be specified with high precision, [4] but subsequently it was shown that, by using a heavy path decomposition of a spanning tree of the network, it is possible to represent each node succinctly, using only a logarithmic number of bits per point. [3] In contrast, there exist graphs that have greedy embeddings in the Euclidean plane, but for which any such embedding requires a polynomial number of bits for the Cartesian coordinates of each point. [5] [6]

Special classes of graphs

Trees

The class of trees that admit greedy embeddings into the Euclidean plane has been completely characterized, and a greedy embedding of a tree can be found in linear time when it exists. [7]

For more general graphs, some greedy embedding algorithms such as the one by Kleinberg [4] start by finding a spanning tree of the given graph, and then construct a greedy embedding of the spanning tree. The result is necessarily also a greedy embedding of the whole graph. However, there exist graphs that have a greedy embedding in the Euclidean plane but for which no spanning tree has a greedy embedding. [8]

Planar graphs

Unsolved problem in mathematics:

Does every polyhedral graph have a planar greedy embedding with convex faces?

(more unsolved problems in mathematics)

Papadimitriou & Ratajczak (2005) conjectured that every polyhedral graph (a 3-vertex-connected planar graph, or equivalently by Steinitz's theorem the graph of a convex polyhedron) has a greedy embedding into the Euclidean plane. [2] By exploiting the properties of cactus graphs, Leighton & Moitra (2010) proved the conjecture; [8] [9] the greedy embeddings of these graphs can be defined succinctly, with logarithmically many bits per coordinate. [10] However, the greedy embeddings constructed according to this proof are not necessarily planar embeddings, as they may include crossings between pairs of edges. For maximal planar graphs, in which every face is a triangle, a greedy planar embedding can be found by applying the Knaster–Kuratowski–Mazurkiewicz lemma to a weighted version of a straight-line embedding algorithm of Schnyder. [11] [12] The strong Papadimitriou–Ratajczak conjecture, that every polyhedral graph has a planar greedy embedding in which all faces are convex, remains unproven. [13]

Unit disk graphs

The wireless sensor networks that are the target of greedy embedding algorithms are frequently modeled as unit disk graphs, graphs in which each node is represented as a unit disk and each edge corresponds to a pair of disks with nonempty intersection. For this special class of graphs, it is possible to find succinct greedy embeddings into a Euclidean space of polylogarithmic dimension, with the additional property that distances in the graph are accurately approximated by distances in the embedding, so that the paths followed by greedy routing are short. [14]

Related Research Articles

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

<span class="mw-page-title-main">Graph drawing</span> Visualization of node-link graphs

Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics.

<span class="mw-page-title-main">Euclidean minimum spanning tree</span> Shortest network connecting points

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

<span class="mw-page-title-main">Spatial network</span> Network representing spatial objects

A spatial network is a graph in which the vertices or edges are spatial elements associated with geometric objects, i.e., the nodes are located in a space equipped with a certain metric. The simplest mathematical realization of spatial network is a lattice or a random geometric graph, where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transportation and mobility networks, Internet, mobile phone networks, power grids, social and contact networks and biological neural networks are all examples where the underlying space is relevant and where the graph's topology alone does not contain all the information. Characterizing and understanding the structure, resilience and the evolution of spatial networks is crucial for many different fields ranging from urbanism to epidemiology.

<span class="mw-page-title-main">Geometric graph theory</span> Subfield of graph theory

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices; thus, it can be described as "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.

<span class="mw-page-title-main">Graph embedding</span> Embedding a graph in a topological space, often Euclidean

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

<span class="mw-page-title-main">Cactus graph</span> Mathematical tree of cycles

In graph theory, a cactus is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, it is a connected graph in which every edge belongs to at most one simple cycle, or in which every block is an edge or a cycle.

<span class="mw-page-title-main">Euclidean shortest path</span> Problem of computing shortest paths around geometric obstacles

The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles.

A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.

<span class="mw-page-title-main">Circle packing theorem</span> Describes the possible tangency relations between circles with disjoint interiors

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.

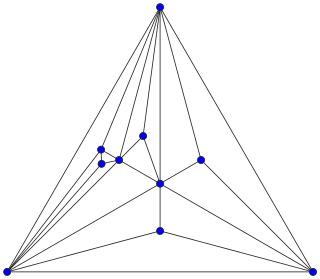
<span class="mw-page-title-main">Apollonian network</span> Graph formed by subdivision of triangles

In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

<span class="mw-page-title-main">1-planar graph</span>

In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.

In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

In combinatorial mathematics and theoretical computer science, heavy-light decomposition is a technique for decomposing a rooted tree into a set of paths. In a heavy path decomposition, each non-leaf node selects one "heavy edge", the edge to the child that has the greatest number of descendants. The selected edges form the paths of the decomposition.

<span class="mw-page-title-main">Upward planar drawing</span> Graph with edges non-crossing and upward

In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint. In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.

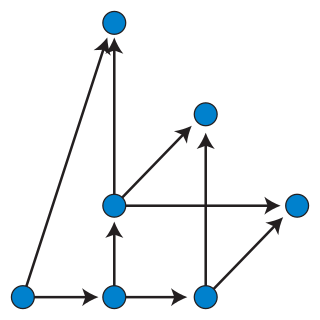
<span class="mw-page-title-main">Dominance drawing</span> Graph where coordinates show reachability

Dominance drawing is a style of graph drawing of directed acyclic graphs that makes the reachability relations between vertices visually apparent. In dominance drawing, vertices are placed at distinct points of the Euclidean plane and a vertex v is reachable from another vertex u if and only if both Cartesian coordinates of v are greater than or equal to the coordinates of u. The edges of a dominance drawing may be drawn either as straight line segments, or, in some cases, as polygonal chains.

In graph drawing, the area used by a drawing is a commonly used way of measuring its quality.

<span class="mw-page-title-main">Hyperbolic geometric graph</span>

A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is a special type of spatial network where (1) latent coordinates of nodes are sprinkled according to a probability density function into a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric (typically either a Heaviside step function resulting in deterministic connections between vertices closer than a certain threshold distance, or a decaying function of hyperbolic distance yielding the connection probability). A HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.

Simultaneous embedding is a technique in graph drawing and information visualization for visualizing two or more different graphs on the same or overlapping sets of labeled vertices, while avoiding crossings within both graphs. Crossings between an edge of one graph and an edge of the other graph are allowed.

References

  1. ↑ Rao, Ananth; Ratnasamy, Sylvia; Papadimitriou, Christos H.; Shenker, Scott; Stoica, Ion (2003), "Geographic routing without location information", Proc. 9th ACM Mobile Computing and Networking (MobiCom), pp. 96–108, doi:10.1145/938985.938996, S2CID   8374920 .
  2. 1 2 3 Papadimitriou, Christos H.; Ratajczak, David (2005), "On a conjecture related to geometric routing", Theoretical Computer Science , 344 (1): 3–14, doi: 10.1016/j.tcs.2005.06.022 , MR   2178923 .
  3. 1 2 Eppstein, D.; Goodrich, M. T. (2011), "Succinct greedy geometric routing using hyperbolic geometry", IEEE Transactions on Computers , 60 (11): 1571–1580, doi:10.1109/TC.2010.257, S2CID   40368995 .
  4. 1 2 Kleinberg, R. (2007), "Geographic routing using hyperbolic space", Proc. 26th IEEE International Conference on Computer Communications (INFOCOM 2007), pp. 1902–1909, doi:10.1109/INFCOM.2007.221, S2CID   11845175 .
  5. ↑ Cao, Lei; Strelzoff, A.; Sun, J. Z. (2009), "On succinctness of geometric greedy routing in Euclidean plane", 10th International Symposium on Pervasive Systems, Algorithms, and Networks (ISPAN 2009), pp. 326–331, doi:10.1109/I-SPAN.2009.20, S2CID   6513298 .
  6. ↑ Angelini, Patrizio; Di Battista, Giuseppe; Frati, Fabrizio (2010), "Succinct greedy drawings do not always exist", Graph Drawing: 17th International Symposium, GD 2009, Chicago, IL, USA, September 22-25, 2009, Revised Papers, Lecture Notes in Computer Science, vol. 5849, pp. 171–182, doi: 10.1007/978-3-642-11805-0_17 , ISBN   978-3-642-11804-3 .
  7. ↑ Nöllenburg, Martin; Prutkin, Roman (2013), "Euclidean greedy drawings of trees", Proc. 21st European Symposium on Algorithms (ESA 2013), arXiv: 1306.5224 , Bibcode:2013arXiv1306.5224N .
  8. 1 2 Leighton, Tom; Moitra, Ankur (2010), "Some results on greedy embeddings in metric spaces", Discrete and Computational Geometry , 44 (3): 686–705, doi: 10.1007/s00454-009-9227-6 , MR   2679063 .
  9. ↑ Angelini, Patrizio; Frati, Fabrizio; Grilli, Luca (2010), "An algorithm to construct greedy drawings of triangulations", Journal of Graph Algorithms and Applications , 14 (1): 19–51, doi: 10.7155/jgaa.00197 , MR   2595019 .
  10. ↑ Goodrich, Michael T.; Strash, Darren (2009), "Succinct greedy geometric routing in the Euclidean plane", Algorithms and Computation: 20th International Symposium, ISAAC 2009, Honolulu, Hawaii, USA, December 16-18, 2009, Proceedings, Lecture Notes in Computer Science, vol. 5878, Berlin: Springer, pp. 781–791, arXiv: 0812.3893 , doi:10.1007/978-3-642-10631-6_79, ISBN   978-3-642-10630-9, MR   2792775, S2CID   15026956 .
  11. ↑ Schnyder, Walter (1990), "Embedding planar graphs on the grid", Proc. 1st ACM/SIAM Symposium on Discrete Algorithms (SODA), pp. 138–148.
  12. ↑ Dhandapani, Raghavan (2010), "Greedy drawings of triangulations", Discrete and Computational Geometry , 43 (2): 375–392, doi:10.1007/s00454-009-9235-6, MR   2579703, S2CID   11617189 . See also
  13. ↑ Nöllenburg, Martin; Prutkin, Roman; Rutter, Ignaz (2016), "On self-approaching and increasing-chord drawings of 3-connected planar graphs", Journal of Computational Geometry, 7 (1): 47–69, arXiv: 1409.0315 , doi:10.20382/jocg.v7i1a3, MR   3463906, S2CID   1500695 .
  14. ↑ Flury, R.; Pemmaraju, S.V.; Wattenhofer, R. (2009), "Greedy routing with bounded stretch", IEEE Infocom 2009, pp. 1737–1745, doi:10.1109/INFCOM.2009.5062093, ISBN   978-1-4244-3512-8, S2CID   1881560 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.