
In mathematics and more specifically in topology, a homeomorphism, also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer . That is,

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In geometric topology, a field within mathematics, the obstruction to a homotopy equivalence of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion which is an element in the Whitehead group. These concepts are named after the mathematician J. H. C. Whitehead.
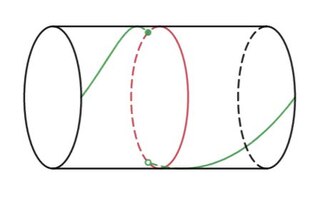
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface.
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.

A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions.
In an area of mathematics called differential topology, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere. That is, M is a sphere from the point of view of all its topological properties, but carrying a smooth structure that is not the familiar one.
In mathematics, a 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different. There exist some topological 4-manifolds which admit no smooth structure, and even if there exists a smooth structure, it need not be unique.

In mathematics, triangulation describes the replacement of topological spaces with simplicial complexes by the choice of an appropriate homeomorphism. A space that admits such a homeomorphism is called a triangulable space. Triangulations can also be used to define a piecewise linear structure for a space, if one exists. Triangulation has various applications both in and outside of mathematics, for instance in algebraic topology, in complex analysis, and in modeling.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.
In topology, a topological manifold is a topological space that locally resembles real n-dimensional Euclidean space. Topological manifolds are an important class of topological spaces, with applications throughout mathematics. All manifolds are topological manifolds by definition. Other types of manifolds are formed by adding structure to a topological manifold. Every manifold has an "underlying" topological manifold, obtained by simply "forgetting" the added structure. However, not every topological manifold can be endowed with a particular additional structure. For example, the E8 manifold is a topological manifold which cannot be endowed with a differentiable structure.
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions. This is slightly stronger than the topological notion of a triangulation. An isomorphism of PL manifolds is called a PL homeomorphism.
In mathematics, more specifically in geometric topology, the Kirby–Siebenmann class is an obstruction for topological manifolds to allow a PL-structure.
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one finite-dimensional manifold from another in a 'controlled' way, introduced by John Milnor. Milnor called this technique surgery, while Andrew Wallace called it spherical modification. The "surgery" on a differentiable manifold M of dimension , could be described as removing an imbedded sphere of dimension p from M. Originally developed for differentiable manifolds, surgery techniques also apply to piecewise linear (PL-) and topological manifolds.
In algebraic geometry, the Iitaka dimension of a line bundle L on an algebraic variety X is the dimension of the image of the rational map to projective space determined by L. This is 1 less than the dimension of the section ring of L
In mathematics, the surgery structure set is the basic object in the study of manifolds which are homotopy equivalent to a closed manifold X. It is a concept which helps to answer the question whether two homotopy equivalent manifolds are diffeomorphic. There are different versions of the structure set depending on the category and whether Whitehead torsion is taken into account or not.
In the mathematical surgery theory the surgery exact sequence is the main technical tool to calculate the surgery structure set of a compact manifold in dimension . The surgery structure set of a compact -dimensional manifold is a pointed set which classifies -dimensional manifolds within the homotopy type of .
In mathematics, the annulus theorem states roughly that the region between two well-behaved spheres is an annulus. It is closely related to the stable homeomorphism conjecture which states that every orientation-preserving homeomorphism of Euclidean space is stable.
This is a glossary of properties and concepts in algebraic topology in mathematics.


















