In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles. Antiprisms are a subclass of the prismatoids and are a (degenerate) type of snub polyhedra.

In geometry, a cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is the only radially equilateral convex polyhedron.
In geometry, a dodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, a Johnson solid is a strictly convex polyhedron, which is not uniform, and each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides (J1); it has 1 square face and 4 triangular faces.

In geometry, a hexagon is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
In geometry, three or more than three straight lines make a polygon and an equilateral polygon is a polygon which has all sides of the same length. Except in the triangle case, it need not be equiangular, but if it does then it is a regular polygon. If the number of sides is at least five, an equilateral polygon need not be a convex polygon: it could be concave or even self-intersecting.

In geometry, a deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces. The number of faces, edges, and vertices is listed below for each of the eight convex deltahedra.

In geometry, a cupola is a solid formed by joining two polygons, one with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively.

In geometry, the pentagonal cupola is one of the Johnson solids (J5). It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.

In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with polygonal base. A pyramid with an n-sided base has n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-dual.
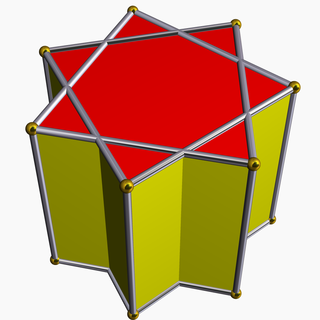
In geometry, the {7/2} heptagrammic prism is one of an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two {7/2} heptagrams.

In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a p-gonal antiprismatic prism is [2p,2+,2], order 8p.
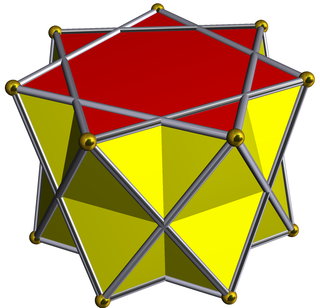
In geometry, the {7/2} heptagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two {7/2} heptagrams.
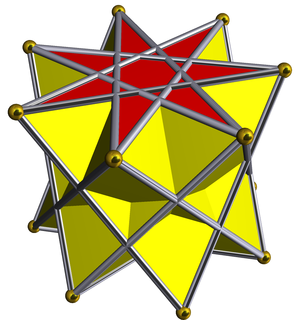
In geometry, the {7/3} heptagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two {7/3} heptagrams.
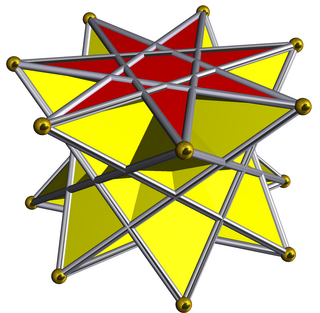
In geometry, the heptagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two {7/3} heptagrams.
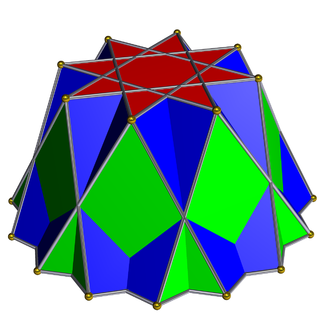
In geometry, the octagrammic cupola is a star-cupola made from an octagram, {8/3} and parallel hexadecagram, {16/3}, connected by 8 equilateral triangles and squares.