In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ; it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform before they refer to it as a “Johnson solid”.

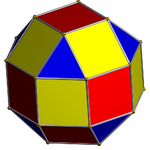
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, a cupola is a solid formed by joining two polygons, one with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively.

In geometry, the triangular cupola is one of the Johnson solids. It can be seen as half a cuboctahedron.

In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids. It can be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagon.

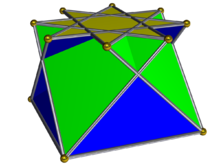
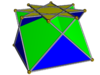
In geometry, the elongated square cupola is one of the Johnson solids. As the name suggests, it can be constructed by elongating a square cupola by attaching an octagonal prism to its base. The solid can be seen as a rhombicuboctahedron with its "lid" removed.

In geometry, the elongated square gyrobicupola or pseudo-rhombicuboctahedron is one of the Johnson solids. It is not usually considered to be an Archimedean solid, even though its faces consist of regular polygons that meet in the same pattern at each of its vertices, because unlike the 13 Archimedean solids, it lacks a set of global symmetries that map every vertex to every other vertex. It strongly resembles, but should not be mistaken for, the rhombicuboctahedron, which is an Archimedean solid. It is also a canonical polyhedron.

In geometry, the square orthobicupola is one of the Johnson solids. As the name suggests, it can be constructed by joining two square cupolae along their octagonal bases, matching like faces. A 45-degree rotation of one cupola before the joining yields a square gyrobicupola.

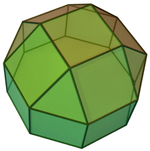
In geometry, the pentagonal cupola is one of the Johnson solids. It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.
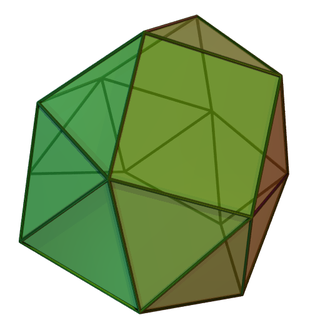
In geometry, the gyroelongated triangular cupola is one of the Johnson solids (J22). It can be constructed by attaching a hexagonal antiprism to the base of a triangular cupola (J3). This is called "gyroelongation", which means that an antiprism is joined to the base of a solid, or between the bases of more than one solid.
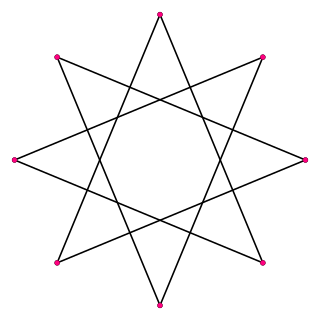
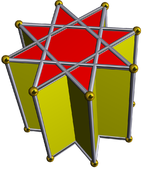
In geometry, an octagram is an eight-angled star polygon.
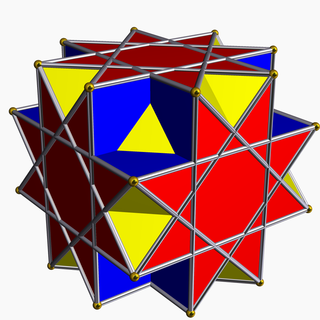
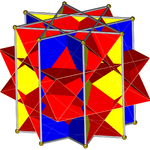
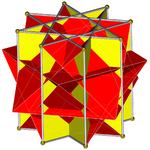
In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14. It has 20 faces (8 triangles, 6 squares and 6 octagrams), 48 edges, and 24 vertices. Its square faces and its octagrammic faces are parallel to those of a cube, while its triangular faces are parallel to those of an octahedron: hence the name cubicuboctahedron. The great suffix serves to distinguish it from the small cubicuboctahedron, which also has faces in the aforementioned directions.
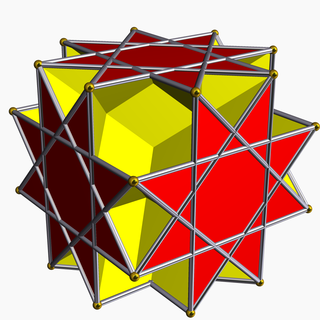
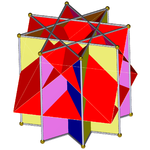
In geometry, the great rhombihexahedron (or great rhombicube) is a nonconvex uniform polyhedron, indexed as U21. It has 18 faces (12 squares and 6 octagrams), 48 edges, and 24 vertices. Its dual is the great rhombihexacron. Its vertex figure is a crossed quadrilateral.
A pseudo-uniform polyhedron is a polyhedron which has regular polygons as faces and has the same vertex configuration at all vertices but is not vertex-transitive: it is not true that for any two vertices, there exists a symmetry of the polyhedron mapping the first isometrically onto the second. Thus, although all the vertices of a pseudo-uniform polyhedron appear the same, it is not isogonal. They are called pseudo-uniform polyhedra due to their resemblance to some true uniform polyhedra.

In geometry, the crossed pentagonal cupoloid or crossed pentagonal semicupola is one member of the infinite family of cuploids. It can be obtained as a slice of the great complex rhombicosidodecahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; but in this case the base polygon is a degenerate {10/4} decagram, as the top is a {5/4} pentagon. Hence, the degenerate base is withdrawn and the triangles are connected to the squares instead.
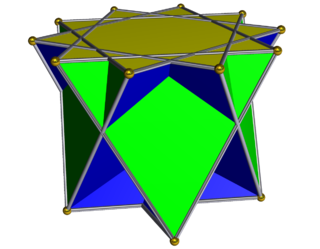
In geometry, the crossed pentagrammic cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex pentagonal cupola. It can be obtained as a slice of the great rhombicosidodecahedron or quasirhombicosidodecahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is a decagram.
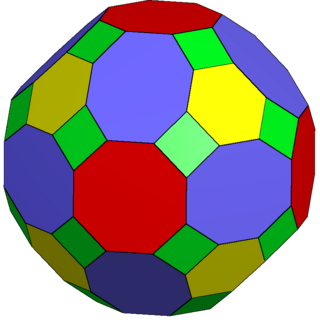
The truncated rhombicuboctahedron is a polyhedron, constructed as a truncation of the rhombicuboctahedron. It has 50 faces consisting of 18 octagons, 8 hexagons, and 24 squares. It can fill space with the truncated cube, truncated tetrahedron and triangular prism as a truncated runcic cubic honeycomb.