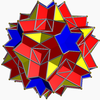
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ; it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform before they refer to it as a “Johnson solid”.

In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.

In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids. It can be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagon.

In geometry, the elongated square gyrobicupola or pseudo-rhombicuboctahedron is one of the Johnson solids. It is not usually considered to be an Archimedean solid, even though its faces consist of regular polygons that meet in the same pattern at each of its vertices, because unlike the 13 Archimedean solids, it lacks a set of global symmetries that map every vertex to every other vertex. It strongly resembles, but should not be mistaken for, the rhombicuboctahedron, which is an Archimedean solid. It is also a canonical polyhedron.

In geometry, the pentagonal cupola is one of the Johnson solids. It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.

In geometry, the diminished rhombicosidodecahedron is one of the Johnson solids. It can be constructed as a rhombicosidodecahedron with one pentagonal cupola removed.

In geometry, the gyrate rhombicosidodecahedron is one of the Johnson solids. It is also a canonical polyhedron.

In geometry, the metabidiminished rhombicosidodecahedron is one of the Johnson solids.

In geometry, the tridiminished rhombicosidodecahedron is one of the Johnson solids. It can be constructed as a rhombicosidodecahedron with three pentagonal cupolae removed.

In geometry, the trigyrate rhombicosidodecahedron is one of the Johnson solids. It contains 20 triangles, 30 squares and 12 pentagons. It is also a canonical polyhedron.

In geometry, the parabigyrate rhombicosidodecahedron is one of the Johnson solids. It can be constructed as a rhombicosidodecahedron with two opposing pentagonal cupolae rotated through 36 degrees. It is also a canonical polyhedron.
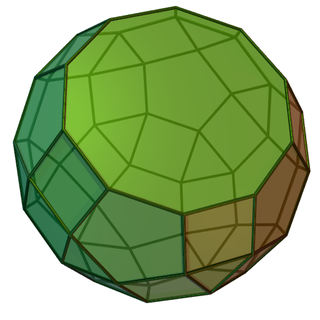
In geometry, the metagyrate diminished rhombicosidodecahedron is one of the Johnson solids. It can be constructed as a rhombicosidodecahedron with one pentagonal cupola rotated through 36 degrees, and a non-opposing pentagonal cupola removed.

In geometry, the bigyrate diminished rhombicosidodecahedron is one of the Johnson solids. It can be constructed as a rhombicosidodecahedron with two pentagonal cupolae rotated through 36 degrees, and a third pentagonal cupola removed.

In geometry, the gyrate bidiminished rhombicosidodecahedron is one of the Johnson solids.
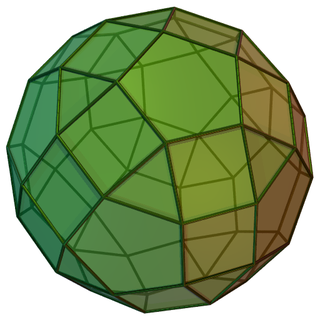
In geometry, the metabigyrate rhombicosidodecahedron is one of the Johnson solids. It can be constructed as a rhombicosidodecahedron with two non-opposing pentagonal cupolae rotated through 36 degrees. It is also a canonical polyhedron.

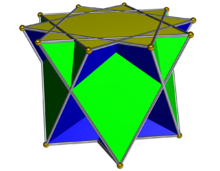
In geometry, the crossed square cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex square cupola. It can be obtained as a slice of the nonconvex great rhombicuboctahedron or quasirhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagram.
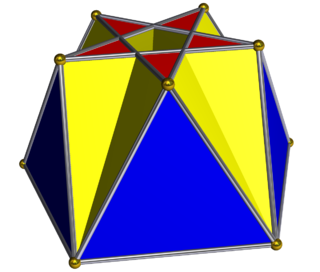
In geometry, the pentagrammic cuploid or pentagrammmic semicupola is the simplest of the infinite family of cuploids. It can be obtained as a slice of the small complex rhombicosidodecahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; but in this case the base polygon is a degenerate {10/2} decagram, as the top is a {5/2} pentagram. Hence, the degenerate base is withdrawn and the triangles are connected to the squares instead.

In geometry, the crossed pentagonal cupoloid or crossed pentagonal semicupola is one member of the infinite family of cuploids. It can be obtained as a slice of the great complex rhombicosidodecahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; but in this case the base polygon is a degenerate {10/4} decagram, as the top is a {5/4} pentagon. Hence, the degenerate base is withdrawn and the triangles are connected to the squares instead.