A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ; it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform before they refer to it as a "Johnson solid".

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

In four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.

In geometry, a cupola is a solid formed by joining two polygons, one with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively.

In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid [sic?].

In geometry, the square cupola the cupola with octagonal base. In the case of edges are equal in length, it is the Johnson solid, a convex polyhedron with faces are regular. It can be considered as half of the rhombicuboctahedron. It can be used to construct many polyhedrons, particularly in other Johnson solids.

In geometry, the pentagonal cupola is one of the Johnson solids. It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.

In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal then it is a regular polygon. Isogonal polygons are equiangular polygons which alternate two edge lengths.
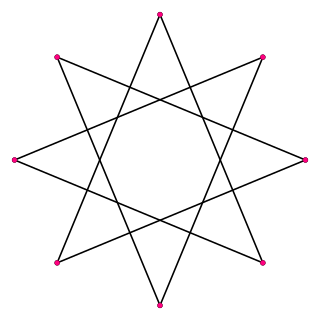
In geometry, an octagram is an eight-angled star polygon.

In mathematics, a hexadecagon is a sixteen-sided polygon.

In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a p-gonal antiprismatic prism is [2p,2+,2], order 8p.
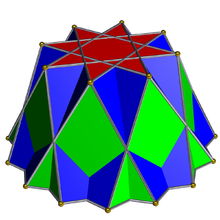
In geometry, the octagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two octagrams.
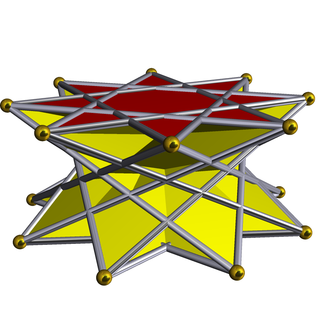
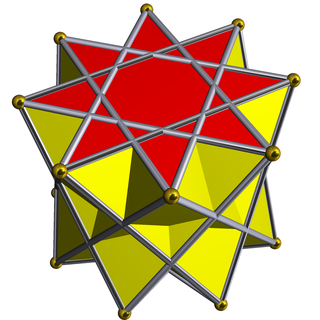
In geometry, the octagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two octagrams.

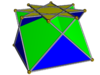
In geometry, the crossed square cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex square cupola. It can be obtained as a slice of the nonconvex great rhombicuboctahedron or quasirhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagram.

In geometry, the heptagrammic cupola is a star-cupola made from a heptagram, {7/3} and parallel tetradecagram, {14/3}, connected by 7 mutually intersecting equilateral triangles and squares.