Level of detail (computer graphics)

In computer graphics, level of detail (LOD) refers to the complexity of a 3D model representation. ^{[1] [2] [3]} LOD can be decreased as the model moves away from the viewer or according to other metrics such as object importance, viewpoint-relative speed or position. LOD techniques increase the efficiency of rendering by decreasing the workload on graphics pipeline stages, usually vertex transformations. The reduced visual quality of the model is often unnoticed because of the small effect on object appearance when distant or moving fast.

Although most of the time LOD is applied to geometry detail only, the basic concept can be generalized. Recently, LOD techniques also included shader management to keep control of pixel complexity. A form of level of detail management has been applied to texture maps for years, under the name of mipmapping, also providing higher rendering quality.

It is commonplace to say that "an object has been LOD-ed" when the object is simplified by the underlying LOD-ing algorithm as well as a 3D modeler manually creating LOD models.^{[ citation needed ]}

Historical reference

The origin of all the LOD algorithms for 3D computer graphics can be traced back to an article by James H. Clark in the October 1976 issue of Communications of the ACM . At the time, computers were monolithic and rare, and graphics were being driven by researchers. The hardware itself was completely different, both architecturally and performance-wise. As such, many differences could be observed with regard to today's algorithms but also many common points.

The original algorithm presented a much more generic approach to what will be discussed here. After introducing some available algorithms for geometry management, it is stated that most fruitful gains came from "...structuring the environments being rendered", allowing to exploit faster transformations and clipping operations.

The same environment structuring is now proposed as a way to control varying detail thus avoiding unnecessary computations, yet delivering adequate visual quality:

For example, a dodecahedron looks like a sphere from a sufficiently large distance and thus can be used to model it so long as it is viewed from that or a greater distance. However, if it must ever be viewed more closely, it will look like a dodecahedron. One solution to this is simply to define it with the most detail that will ever be necessary. However, then it might have far more detail than is needed to represent it at large distances, and in a complex environment with many such objects, there would be too many polygons (or other geometric primitives) for the visible surface algorithms to efficiently handle.

The proposed algorithm envisions a tree data structure which encodes in its arcs both transformations and transitions to more detailed objects. In this way, each node encodes an object and according to a fast heuristic, the tree is descended to the leaves which provide each object with more detail. When a leaf is reached, other methods could be used when higher detail is needed, such as Catmull's recursive subdivision .

The significant point, however, is that in a complex environment, the amount of information presented about the various objects in the environment varies according to the fraction of the field of view occupied by those objects.

The paper then introduces clipping (not to be confused with culling although often similar), various considerations on the graphical working set and its impact on performance, interactions between the proposed algorithm and others to improve rendering speed.

Well known approaches

Although the algorithm introduced above covers a whole range of level of detail management techniques, real world applications usually employ specialized methods tailored to the information being rendered. Depending on the requirements of the situation, two main methods are used:

The first method, Discrete Levels of Detail (DLOD), involves creating multiple, discrete versions of the original geometry with decreased levels of geometric detail. At runtime, the full-detail models are substituted for the models with reduced detail as necessary. Due to the discrete nature of the levels, there may be visual popping when one model is exchanged for another. This may be mitigated by alpha blending or morphing between states during the transition.

The second method, Continuous Levels of Detail (CLOD), uses a structure which contains a continuously variable spectrum of geometric detail. The structure can then be probed to smoothly choose the appropriate level of detail required for the situation. A significant advantage of this technique is the ability to locally vary the detail; for instance, the side of a large object nearer to the view may be presented in high detail, while simultaneously reducing the detail on its distant side.

In both cases, LODs are chosen based on some heuristic which is used to judge how much detail is being lost by the reduction in detail, such as by evaluation of the LOD's geometric error relative to the full-detail model. Objects are then displayed with the minimum amount of detail required to satisfy the heuristic, which is designed to minimize geometric detail as much as possible to maximize performance while maintaining an acceptable level of visual quality.

Details on discrete LOD

An example of various DLOD ranges. Darker areas are meant to be rendered with higher detail. An additional culling operation is run, discarding all the information outside the frustum (colored areas).

The basic concept of discrete LOD (DLOD) is to provide various models to represent the same object. Obtaining those models requires an external algorithm which is often non-trivial and subject of many polygon reduction techniques. Successive LOD-ing algorithms will simply assume those models are available.

DLOD algorithms are often used in performance-intensive applications with small data sets which can easily fit in memory. Although out-of-core algorithms could be used, the information granularity is not well suited to this kind of application. This kind of algorithm is usually easier to get working, providing both faster performance and lower CPU usage because of the few operations involved.

DLOD methods are often used for "stand-alone" moving objects, possibly including complex animation methods. A different approach is used for geomipmapping, a popular terrain rendering algorithm because this applies to terrain meshes which are both graphically and topologically different from "object" meshes. Instead of computing an error and simplify the mesh according to this, geomipmapping takes a fixed reduction method, evaluates the error introduced and computes a distance at which the error is acceptable. Although straightforward, the algorithm provides decent performance.

A discrete LOD example

As a simple example, consider a sphere. A discrete LOD approach would cache a certain number of models to be used at different distances. Because the model can trivially be procedurally generated by its mathematical formulation, using a different number of sample points distributed on the surface is sufficient to generate the various models required. This pass is not a LOD-ing algorithm.

Visual impact comparisons and measurements

Image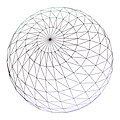
Vertices	~5500	~2880	~1580	~670	140
Notes	Maximum detail, for closeups				Minimum detail, very far objects

To simulate a realistic transform bound scenario, an ad-hoc written application can be used. The use of simple algorithms and minimum fragment operations ensures that CPU bounding does not occur. Each frame, the program will compute each sphere's distance and choose a model from a pool according to this information. To easily show the concept, the distance at which each model is used is hard coded in the source. A more involved method would compute adequate models according to the usage distance chosen.

OpenGL is used for rendering due to its high efficiency in managing small batches, storing each model in a display list thus avoiding communication overheads. Additional vertex load is given by applying two directional light sources ideally located infinitely far away.

The following table compares the performance of LOD aware rendering and a full detail (brute force) method.

Visual impact comparisons and measurements

	Brute	DLOD	Comparison
Rendered images
Render time	27.27 ms	1.29 ms	21 × reduction
Scene vertices	2,328,480	109,440	21 × reduction

Hierarchical LOD

Because hardware is geared towards large amounts of detail, rendering low polygon objects may score sub-optimal performances. HLOD avoids the problem by grouping different objects together . This allows for higher efficiency as well as taking advantage of proximity considerations.

Practical applications

Video games

LOD is especially useful in 3D video games. Video game developers want to provide players with large worlds but are always constrained by hardware, frame rate and the real-time nature of video game graphics. With the advent of 3D games in the 1990s, a lot of video games simply did not render distant structures or objects. Only nearby objects would be rendered and more distant parts would gradually fade, essentially implementing distance fog. Video games using LOD rendering avoid this fog effect and can render larger areas. Some notable early examples of LOD rendering in 3D video games include The Killing Cloud , Spyro the Dragon , Crash Bandicoot: Warped , Unreal Tournament and the Serious Sam engine. Most modern 3D games use a combination of LOD rendering techniques, using different models for large structures and distance culling for environment details like grass and trees. The effect is sometimes still noticeable, for example when the player character flies over the virtual terrain or uses a sniper scope for long distance viewing. Especially grass and foliage will seem to pop-up when getting closer, also known as foliage culling. ^[4] LOD can also be used to render fractal terrain in real time. ^[5] Unreal Engine 5's Nanite system essentially implements level-of-detail within meshes instead of just objects as a whole.

In GIS and 3D city modelling

LOD is found in GIS and 3D city models as a similar concept. It indicates how thoroughly real-world features have been mapped and how much the model adheres to its real-world counterpart. Besides the geometric complexity, other metrics such as spatio-semantic coherence, resolution of the texture and attributes can be considered in the LOD of a model. The standard CityGML contains one of the most prominent LOD categorizations.

The analogy of "LOD-ing" in GIS is referred to as generalization.

Rendering and modeling software

• MeshLab an open source mesh processing tool that is able to accurately simplify 3D polygonal meshes.
• Polygon Cruncher a commercial software from Mootools that reduces the number of polygons of objects without changing their appearance.
• Simplygon a commercial mesh processing package for remeshing general input meshes into real-time renderable meshes.

See also

• Anisotropic filtering
• Distance fog
• Draw distance
• Mipmap
• Popping (computer graphics)
• Progressive meshes
• Sparse voxel octree
• Spatial resolution

References

1. "Multiple levels of detail" (PDF). clemson.edu. Retrieved 2 July 2023.
2. "Levels of Detail LOD" (PDF). computer-graphics.se. Retrieved 2 July 2023.
3. "GPU based dynamic geometry LOD – RasterGrid".
4. "Foliage Mode". docs.unrealengine.com. Retrieved 2 July 2023.
5. "Musgrave, F. Kenton, Craig E. Kolb, and Robert S. Mace. "The synthesis and rendering of eroded fractal terrains." ACM Siggraph Computer Graphics. Vol. 23. No. 3. ACM, 1989" (PDF). Retrieved 2 July 2023.

1. ^ Communications of the ACM, October 1976 Volume 19 Number 10. Pages 547–554. Hierarchical Geometric Models for Visible Surface Algorithms by James H. Clark, University of California at Santa Cruz. Digitalized scan is freely available at https://web.archive.org/web/20060910212907/http://accad.osu.edu/%7Ewaynec/history/PDFs/clark-vis-surface.pdf.
2. ^ Catmull E., A Subdivision Algorithm for Computer Display of Curved Surfaces. Tech. Rep. UTEC-CSc-74-133, University of Utah, Salt Lake City, Utah, Dec. 1
3. ^ Ribelles, López, and Belmonte, "An Improved Discrete Level of Detail Model Through an Incremental Representation", 2010, Available at http://www3.uji.es/~ribelles/papers/2010-TPCG/tpcg10.pdf
4. ^ de Boer, W.H., Fast Terrain Rendering using Geometrical Mipmapping, in flipCode featured articles, October 2000. Available at flipcode - Fast Terrain Rendering Using Geometrical MipMapping.
5. ^ Carl Erikson's paper at http://www.cs.unc.edu/Research/ProjectSummaries/hlods.pdf provides a quick, yet effective overlook at HLOD mechanisms. A more involved description follows in his thesis, at https://wwwx.cs.unc.edu/~geom/papers/documents/dissertations/erikson00.pdf.