A coordination complex is a chemical compound consisting of a central atom or ion, which is usually metallic and is called the coordination centre, and a surrounding array of bound molecules or ions, that are in turn known as ligands or complexing agents. Many metal-containing compounds, especially those that include transition metals, are coordination complexes.
In coordination chemistry, a ligand is an ion or molecule with a functional group that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's electron pairs, often through Lewis bases. The nature of metal–ligand bonding can range from covalent to ionic. Furthermore, the metal–ligand bond order can range from one to three. Ligands are viewed as Lewis bases, although rare cases are known to involve Lewis acidic "ligands".
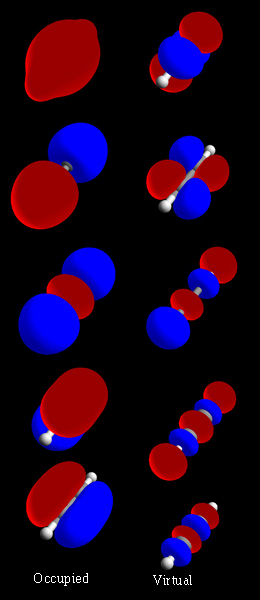
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms atomic orbital and molecular orbital were introduced by Robert S. Mulliken in 1932 to mean one-electron orbital wave functions. At an elementary level, they are used to describe the region of space in which a function has a significant amplitude.

In theoretical chemistry, a conjugated system is a system of connected p-orbitals with delocalized electrons in a molecule, which in general lowers the overall energy of the molecule and increases stability. It is conventionally represented as having alternating single and multiple bonds. Lone pairs, radicals or carbenium ions may be part of the system, which may be cyclic, acyclic, linear or mixed. The term "conjugated" was coined in 1899 by the German chemist Johannes Thiele.
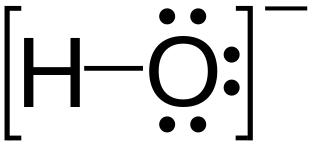
In chemistry, a lone pair refers to a pair of valence electrons that are not shared with another atom in a covalent bond and is sometimes called an unshared pair or non-bonding pair. Lone pairs are found in the outermost electron shell of atoms. They can be identified by using a Lewis structure. Electron pairs are therefore considered lone pairs if two electrons are paired but are not used in chemical bonding. Thus, the number of electrons in lone pairs plus the number of electrons in bonds equals the number of valence electrons around an atom.
In chemistry, molecular orbital theory is a method for describing the electronic structure of molecules using quantum mechanics. It was proposed early in the 20th century.
In molecular physics, crystal field theory (CFT) describes the breaking of degeneracies of electron orbital states, usually d or f orbitals, due to a static electric field produced by a surrounding charge distribution. This theory has been used to describe various spectroscopies of transition metal coordination complexes, in particular optical spectra (colors). CFT successfully accounts for some magnetic properties, colors, hydration enthalpies, and spinel structures of transition metal complexes, but it does not attempt to describe bonding. CFT was developed by physicists Hans Bethe and John Hasbrouck van Vleck in the 1930s. CFT was subsequently combined with molecular orbital theory to form the more realistic and complex ligand field theory (LFT), which delivers insight into the process of chemical bonding in transition metal complexes. CFT can be complicated further by breaking assumptions made of relative metal and ligand orbital energies, requiring the use of inverted ligand field theory (ILFT) to better describe bonding.

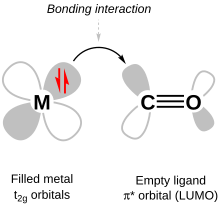
In chemistry, π backbonding, also called π backdonation, is when electrons move from an atomic orbital on one atom to an appropriate symmetry antibonding orbital on a π-acceptor ligand. It is especially common in the organometallic chemistry of transition metals with multi-atomic ligands such as carbon monoxide, ethylene or the nitrosonium cation. Electrons from the metal are used to bond to the ligand, in the process relieving the metal of excess negative charge. Compounds where π backbonding occurs include Ni(CO)4 and Zeise's salt. IUPAC offers the following definition for backbonding:
A description of the bonding of π-conjugated ligands to a transition metal which involves a synergic process with donation of electrons from the filled π-orbital or lone electron pair orbital of the ligand into an empty orbital of the metal (donor–acceptor bond), together with release (back donation) of electrons from an nd orbital of the metal (which is of π-symmetry with respect to the metal–ligand axis) into the empty π*-antibonding orbital of the ligand.
The Jahn–Teller effect is an important mechanism of spontaneous symmetry breaking in molecular and solid-state systems which has far-reaching consequences in different fields, and is responsible for a variety of phenomena in spectroscopy, stereochemistry, crystal chemistry, molecular and solid-state physics, and materials science. The effect is named for Hermann Arthur Jahn and Edward Teller, who first reported studies about it in 1937.

In chemistry, octahedral molecular geometry, also called square bipyramidal, describes the shape of compounds with six atoms or groups of atoms or ligands symmetrically arranged around a central atom, defining the vertices of an octahedron. The octahedron has eight faces, hence the prefix octa. The octahedron is one of the Platonic solids, although octahedral molecules typically have an atom in their centre and no bonds between the ligand atoms. A perfect octahedron belongs to the point group Oh. Examples of octahedral compounds are sulfur hexafluoride SF6 and molybdenum hexacarbonyl Mo(CO)6. The term "octahedral" is used somewhat loosely by chemists, focusing on the geometry of the bonds to the central atom and not considering differences among the ligands themselves. For example, [Co(NH3)6]3+, which is not octahedral in the mathematical sense due to the orientation of the N−H bonds, is referred to as octahedral.

A quintuple bond in chemistry is an unusual type of chemical bond, first reported in 2005 for a dichromium compound. Single bonds, double bonds, and triple bonds are commonplace in chemistry. Quadruple bonds are rarer and are currently known only among the transition metals, especially for Cr, Mo, W, and Re, e.g. [Mo2Cl8]4− and [Re2Cl8]2−. In a quintuple bond, ten electrons participate in bonding between the two metal centers, allocated as σ2π4δ4.

In chemistry, the square planar molecular geometry describes the stereochemistry that is adopted by certain chemical compounds. As the name suggests, molecules of this geometry have their atoms positioned at the corners.
A spectrochemical series is a list of ligands ordered by ligand "strength", and a list of metal ions based on oxidation number, group and element. For a metal ion, the ligands modify the difference in energy Δ between the d orbitals, called the ligand-field splitting parameter in ligand field theory, or the crystal-field splitting parameter in crystal field theory. The splitting parameter is reflected in the ion's electronic and magnetic properties such as its spin state, and optical properties such as its color and absorption spectrum.
The 18-electron rule is a chemical rule of thumb used primarily for predicting and rationalizing formulas for stable transition metal complexes, especially organometallic compounds. The rule is based on the fact that the valence orbitals in the electron configuration of transition metals consist of five (n−1)d orbitals, one ns orbital, and three np orbitals, where n is the principal quantum number. These orbitals can collectively accommodate 18 electrons as either bonding or non-bonding electron pairs. This means that the combination of these nine atomic orbitals with ligand orbitals creates nine molecular orbitals that are either metal-ligand bonding or non-bonding. When a metal complex has 18 valence electrons, it is said to have achieved the same electron configuration as the noble gas in the period, lending stability to the complex. Transition metal complexes that deviate from the rule are often interesting or useful because they tend to be more reactive. The rule is not helpful for complexes of metals that are not transition metals. The rule was first proposed by American chemist Irving Langmuir in 1921.
In coordination chemistry, Tanabe–Sugano diagrams are used to predict absorptions in the ultraviolet (UV), visible and infrared (IR) electromagnetic spectrum of coordination compounds. The results from a Tanabe–Sugano diagram analysis of a metal complex can also be compared to experimental spectroscopic data. They are qualitatively useful and can be used to approximate the value of 10Dq, the ligand field splitting energy. Tanabe–Sugano diagrams can be used for both high spin and low spin complexes, unlike Orgel diagrams, which apply only to high spin complexes. Tanabe–Sugano diagrams can also be used to predict the size of the ligand field necessary to cause high-spin to low-spin transitions.
An electronic effect influences the structure, reactivity, or properties of a molecule but is neither a traditional bond nor a steric effect. In organic chemistry, the term stereoelectronic effect is also used to emphasize the relation between the electronic structure and the geometry (stereochemistry) of a molecule.
The d electron count or number of d electrons is a chemistry formalism used to describe the electron configuration of the valence electrons of a transition metal center in a coordination complex. The d electron count is an effective way to understand the geometry and reactivity of transition metal complexes. The formalism has been incorporated into the two major models used to describe coordination complexes; crystal field theory and ligand field theory, which is a more advanced version based on molecular orbital theory. However the d electron count of an atom in a complex is often different from the d electron count of a free atom or a free ion of the same element.
Spin states when describing transition metal coordination complexes refers to the potential spin configurations of the central metal's d electrons. For several oxidation states, metals can adopt high-spin and low-spin configurations. The ambiguity only applies to first row metals, because second- and third-row metals are invariably low-spin. These configurations can be understood through the two major models used to describe coordination complexes; crystal field theory and ligand field theory.
Magnetochemistry is concerned with the magnetic properties of chemical compounds. Magnetic properties arise from the spin and orbital angular momentum of the electrons contained in a compound. Compounds are diamagnetic when they contain no unpaired electrons. Molecular compounds that contain one or more unpaired electrons are paramagnetic. The magnitude of the paramagnetism is expressed as an effective magnetic moment, μeff. For first-row transition metals the magnitude of μeff is, to a first approximation, a simple function of the number of unpaired electrons, the spin-only formula. In general, spin–orbit coupling causes μeff to deviate from the spin-only formula. For the heavier transition metals, lanthanides and actinides, spin–orbit coupling cannot be ignored. Exchange interaction can occur in clusters and infinite lattices, resulting in ferromagnetism, antiferromagnetism or ferrimagnetism depending on the relative orientations of the individual spins.

Alkaline earth octacarbonyl complexes are a class of neutral compounds that have the general formula M(CO)8 where M is a heavy Group 2 element (Ca, Sr, or Ba). The metal center has a formal oxidation state of 0 and the complex has a high level of symmetry belonging to the cubic Oh point group. These complexes are isolable in a low-temperature neon matrix, but are not frequently used in applications due to their instability in air and water. The bonding within these complexes is controversial with some arguing the bonding resembles a model similar to bonding in transition metal carbonyl complexes which abide by the 18-electron rule, and others arguing the molecule more accurately contains ionic bonds between the alkaline earth metal center and the carbonyl ligands. Complexes of Be(CO)8 and Mg(CO)8 are not synthetically possible due to inaccessible (n-1)d orbitals. Beryllium has been found to form a dinuclear homoleptic carbonyl and magnesium a mononuclear heteroleptic carbonyl, both with only two carbonyl ligands instead of eight to each metal atom.
![Ligand-Field scheme summarizing s-bonding in the octahedral complex [Ti(H2O)6] . LFTi(III).png](http://upload.wikimedia.org/wikipedia/commons/thumb/8/8b/LFTi%28III%29.png/400px-LFTi%28III%29.png)