Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in applied mathematics and in the natural sciences and engineering disciplines, as well as in non-physical systems such as the social sciences. It can also be taught as a subject in its own right.
A proportional–integral–derivative controller is a feedback-based control loop mechanism commonly used to manage machines and processes that require continuous control and automatic adjustment. It is typically used in industrial control systems and various other applications where constant control through modulation is necessary without human intervention. The PID controller automatically compares the desired target value with the actual value of the system. The difference between these two values is called the error value, denoted as .
H∞methods are used in control theory to synthesize controllers to achieve stabilization with guaranteed performance. To use H∞ methods, a control designer expresses the control problem as a mathematical optimization problem and then finds the controller that solves this optimization. H∞ techniques have the advantage over classical control techniques in that H∞ techniques are readily applicable to problems involving multivariate systems with cross-coupling between channels; disadvantages of H∞ techniques include the level of mathematical understanding needed to apply them successfully and the need for a reasonably good model of the system to be controlled. It is important to keep in mind that the resulting controller is only optimal with respect to the prescribed cost function and does not necessarily represent the best controller in terms of the usual performance measures used to evaluate controllers such as settling time, energy expended, etc. Also, non-linear constraints such as saturation are generally not well-handled. These methods were introduced into control theory in the late 1970s-early 1980s by George Zames, J. William Helton , and Allen Tannenbaum.
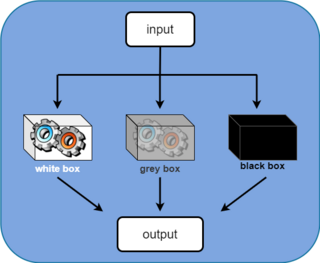
The field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data. System identification also includes the optimal design of experiments for efficiently generating informative data for fitting such models as well as model reduction. A common approach is to start from measurements of the behavior of the system and the external influences and try to determine a mathematical relation between them without going into many details of what is actually happening inside the system; this approach is called black box system identification.
Model predictive control (MPC) is an advanced method of process control that is used to control a process while satisfying a set of constraints. It has been in use in the process industries in chemical plants and oil refineries since the 1980s. In recent years it has also been used in power system balancing models and in power electronics. Model predictive controllers rely on dynamic models of the process, most often linear empirical models obtained by system identification. The main advantage of MPC is the fact that it allows the current timeslot to be optimized, while keeping future timeslots in account. This is achieved by optimizing a finite time-horizon, but only implementing the current timeslot and then optimizing again, repeatedly, thus differing from a linear–quadratic regulator (LQR). Also MPC has the ability to anticipate future events and can take control actions accordingly. PID controllers do not have this predictive ability. MPC is nearly universally implemented as a digital control, although there is research into achieving faster response times with specially designed analog circuitry.
Adaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself to such changing conditions. Adaptive control is different from robust control in that it does not need a priori information about the bounds on these uncertain or time-varying parameters; robust control guarantees that if the changes are within given bounds the control law need not be changed, while adaptive control is concerned with control law changing itself.
In control theory, advanced process control (APC) refers to a broad range of techniques and technologies implemented within industrial process control systems. Advanced process controls are usually deployed optionally and in addition to basic process controls. Basic process controls are designed and built with the process itself, to facilitate basic operation, control and automation requirements. Advanced process controls are typically added subsequently, often over the course of many years, to address particular performance or economic improvement opportunities in the process.
The theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic function is called the LQ problem. One of the main results in the theory is that the solution is provided by the linear–quadratic regulator (LQR), a feedback controller whose equations are given below.
In control theory, the linear–quadratic–Gaussian (LQG) control problem is one of the most fundamental optimal control problems, and it can also be operated repeatedly for model predictive control. It concerns linear systems driven by additive white Gaussian noise. The problem is to determine an output feedback law that is optimal in the sense of minimizing the expected value of a quadratic cost criterion. Output measurements are assumed to be corrupted by Gaussian noise and the initial state, likewise, is assumed to be a Gaussian random vector.
In control theory, gain scheduling is an approach to control of nonlinear systems that uses a family of linear controllers, each of which provides satisfactory control for a different operating point of the system.
Control reconfiguration is an active approach in control theory to achieve fault-tolerant control for dynamic systems. It is used when severe faults, such as actuator or sensor outages, cause a break-up of the control loop, which must be restructured to prevent failure at the system level. In addition to loop restructuring, the controller parameters must be adjusted to accommodate changed plant dynamics. Control reconfiguration is a building block toward increasing the dependability of systems under feedback control.
Stochastic control or stochastic optimal control is a sub field of control theory that deals with the existence of uncertainty either in observations or in the noise that drives the evolution of the system. The system designer assumes, in a Bayesian probability-driven fashion, that random noise with known probability distribution affects the evolution and observation of the state variables. Stochastic control aims to design the time path of the controlled variables that performs the desired control task with minimum cost, somehow defined, despite the presence of this noise. The context may be either discrete time or continuous time.
Moving horizon estimation (MHE) is an optimization approach that uses a series of measurements observed over time, containing noise and other inaccuracies, and produces estimates of unknown variables or parameters. Unlike deterministic approaches, MHE requires an iterative approach that relies on linear programming or nonlinear programming solvers to find a solution.

Wassim Michael Haddad is a Lebanese-Greek-American applied mathematician, scientist, and engineer, with research specialization in the areas of dynamical systems and control. His research has led to fundamental breakthroughs in applied mathematics, thermodynamics, stability theory, robust control, dynamical system theory, and neuroscience. Professor Haddad is a member of the faculty of the School of Aerospace Engineering at Georgia Institute of Technology, where he holds the rank of Professor and Chair of the Flight Mechanics and Control Discipline. Dr. Haddad is a member of the Academy of Nonlinear SciencesArchived 2016-03-04 at the Wayback Machine for recognition of paramount contributions to the fields of nonlinear stability theory, nonlinear dynamical systems, and nonlinear control and an IEEE Fellow for contributions to robust, nonlinear, and hybrid control systems.
Baranyi and Yam proposed the TP model transformation as a new concept in quasi-LPV (qLPV) based control, which plays a central role in the highly desirable bridging between identification and polytopic systems theories. It is also used as a TS (Takagi-Sugeno) fuzzy model transformation. It is uniquely effective in manipulating the convex hull of polytopic forms, and, hence, has revealed and proved the fact that convex hull manipulation is a necessary and crucial step in achieving optimal solutions and decreasing conservativeness in modern linear matrix inequality based control theory. Thus, although it is a transformation in a mathematical sense, it has established a conceptually new direction in control theory and has laid the ground for further new approaches towards optimality.
System identification is a method of identifying or measuring the mathematical model of a system from measurements of the system inputs and outputs. The applications of system identification include any system where the inputs and outputs can be measured and include industrial processes, control systems, economic data, biology and the life sciences, medicine, social systems and many more.
Classical control theory is a branch of control theory that deals with the behavior of dynamical systems with inputs, and how their behavior is modified by feedback, using the Laplace transform as a basic tool to model such systems.
The GEKKO Python package solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers. Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear model predictive control. In addition, the package solves Linear programming (LP), Quadratic programming (QP), Quadratically constrained quadratic program (QCQP), Nonlinear programming (NLP), Mixed integer programming (MIP), and Mixed integer linear programming (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation.
Chance Constrained Programming (CCP) is a mathematical optimization approach used to handle problems under uncertainty. It was first introduced by Charnes and Cooper in 1959 and further developed by Miller and Wagner in 1965. CCP is widely used in various fields, including finance, engineering, and operations research, to optimize decision-making processes where certain constraints need to be satisfied with a specified probability.













