Related Research Articles

In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i.e. that the space not exclude any limiting values of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval [0,1] would be compact. Similarly, the space of rational numbers is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers is not compact either, because it excludes the two limiting values and . However, the extended real number linewould be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topological spaces.
In mathematics, in general topology, compactification is the process or result of making a topological space into a compact space. A compact space is a space in which every open cover of the space contains a finite subcover. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".
In topology and related branches of mathematics, a Hausdorff space ( HOWS-dorf, HOWZ-dorf), separated space or T2 space is a topological space where, for any two distinct points, there exist neighbourhoods of each which are disjoint from each other. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" (T2) is the most frequently used and discussed. It implies the uniqueness of limits of sequences, nets, and filters.
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metric such that the topology induced by is Metrization theorems are theorems that give sufficient conditions for a topological space to be metrizable.
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points, along with an additional structure called a topology, which can be defined as a set of neighbourhoods for each point that satisfy some axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate.
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces. These conditions are examples of separation axioms. A Tychonoff space refers to any completely regular space that is also a Hausdorff space; there exist completely regular spaces that are not Tychonoff.
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space. These conditions are examples of separation axioms and their further strengthenings define completely normal Hausdorff spaces, or T5 spaces, and perfectly normal Hausdorff spaces, or T6 spaces.
In mathematics, a paracompact space is a topological space in which every open cover has an open refinement that is locally finite. These spaces were introduced by Dieudonné (1944). Every compact space is paracompact. Every paracompact Hausdorff space is normal, and a Hausdorff space is paracompact if and only if it admits partitions of unity subordinate to any open cover. Sometimes paracompact spaces are defined so as to always be Hausdorff.
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which every point has a compact neighborhood.
In topology and related fields of mathematics, a topological space X is called a regular space if every closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C can be separated by neighborhoods. This condition is known as Axiom T3. The term "T3 space" usually means "a regular Hausdorff space". These conditions are examples of separation axioms.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology. Another name for general topology is point-set topology.
In topology, a compactly generated space is a topological space whose topology is coherent with the family of all compact subspaces. Specifically, a topological space X is compactly generated if it satisfies the following condition:
In topology and related areas of mathematics, a topological property or topological invariant is a property of a topological space that is invariant under homeomorphisms. Alternatively, a topological property is a proper class of topological spaces which is closed under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic to X possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets.
In topology, a branch of mathematics, a topological manifold is a topological space that locally resembles real n-dimensional Euclidean space. Topological manifolds are an important class of topological spaces, with applications throughout mathematics. All manifolds are topological manifolds by definition. Other types of manifolds are formed by adding structure to a topological manifold. Every manifold has an "underlying" topological manifold, obtained by simply "forgetting" the added structure. However, not every topological manifold can be endowed with a particular additional structure. For example, the E8 manifold is a topological manifold which cannot be endowed with a differentiable structure.
In mathematics, more specifically point-set topology, a Moore space is a developable regular Hausdorff space. That is, a topological space X is a Moore space if the following conditions hold:
In mathematics, a topological space is called collectionwise normal if for every discrete family Fi of closed subsets of there exists a pairwise disjoint family of open sets Ui, such that Fi ⊆ Ui. A family of subsets of is called discrete when every point of has a neighbourhood that intersects at most one of the sets from . An equivalent definition of collectionwise normal demands that the above Ui are themselves a discrete family, which is stronger than pairwise disjoint.
In mathematics, a weak Hausdorff space or weakly Hausdorff space is a topological space where the image of every continuous map from a compact Hausdorff space into the space is closed. In particular, every Hausdorff space is weak Hausdorff. As a separation property, it is stronger than T1, which is equivalent to the statement that points are closed. Specifically, every weak Hausdorff space is a T1 space.
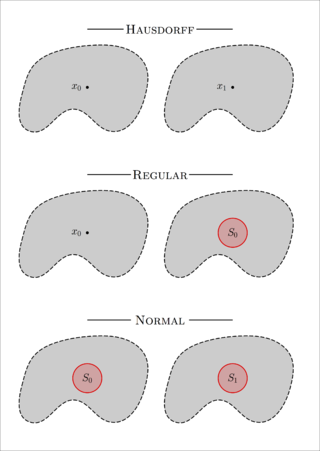
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms. These are sometimes called Tychonoff separation axioms, after Andrey Tychonoff.
References
- ↑ Bella, A.; Carlson, N. (2018-01-02). "On cardinality bounds involving the weak Lindelöf degree". Quaestiones Mathematicae. 41 (1): 99–113. doi:10.2989/16073606.2017.1373157. ISSN 1607-3606. S2CID 119732758.
- ↑ Hansell, R. W.; Jayne, J. E.; Rogers, C. A. (June 1985). "Separation of K –analytic sets". Mathematika . 32 (1): 147–190. doi:10.1112/S0025579300010962. ISSN 0025-5793.