
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations of measure are widely used in quantum physics and physics in general.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.

In mathematics, open sets are a generalization of open intervals in the real line.
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space. These conditions are examples of separation axioms and their further strengthenings define completely normal Hausdorff spaces, or T5 spaces, and perfectly normal Hausdorff spaces, or T6 spaces.
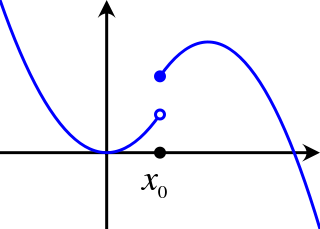
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function is uppersemicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points in the closure of S not belonging to the interior of S. An element of the boundary of S is called a boundary point of S. The term boundary operation refers to finding or taking the boundary of a set. Notations used for boundary of a set S include and . Some authors use the term frontier instead of boundary in an attempt to avoid confusion with a different definition used in algebraic topology and the theory of manifolds. Despite widespread acceptance of the meaning of the terms boundary and frontier, they have sometimes been used to refer to other sets. For example, Metric Spaces by E. T. Copson uses the term boundary to refer to Hausdorff's border, which is defined as the intersection of a set with its boundary. Hausdorff also introduced the term residue, which is defined as the intersection of a set with the closure of the border of its complement.
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.

In mathematics, the symmetric difference of two sets, also known as the disjunctive union, is the set of elements which are in either of the sets, but not in their intersection. For example, the symmetric difference of the sets and is .
In mathematics, Fatou's lemma establishes an inequality relating the Lebesgue integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions. The lemma is named after Pierre Fatou.
In mathematics, more specifically in topology, an open map is a function between two topological spaces that maps open sets to open sets. That is, a function is open if for any open set in the image is open in Likewise, a closed map is a function that maps closed sets to closed sets. A map may be open, closed, both, or neither; in particular, an open map need not be closed and vice versa.
In mathematics, an additive set function is a function mapping sets to numbers, with the property that its value on a union of two disjoint sets equals the sum of its values on these sets, namely, If this additivity property holds for any two sets, then it also holds for any finite number of sets, namely, the function value on the union of k disjoint sets equals the sum of its values on the sets. Therefore, an additive set function is also called a finitely-additive set function. However, a finitely-additive set function might not have the additivity property for a union of an infinite number of sets. A σ-additive set function is a function that has the additivity property even for countably infinite many sets, that is,
Pregeometry, and in full combinatorial pregeometry, are essentially synonyms for "matroid". They were introduced by Gian-Carlo Rota with the intention of providing a less "ineffably cacophonous" alternative term. Also, the term combinatorial geometry, sometimes abbreviated to geometry, was intended to replace "simple matroid". These terms are now infrequently used in the study of matroids.
In mathematics, a π-system on a set is a collection of certain subsets of such that
In the mathematical field of topology, a hyperconnected space or irreducible space is a topological space X that cannot be written as the union of two proper closed sets. The name irreducible space is preferred in algebraic geometry.
In mathematics, a topological space is called collectionwise normal if for every discrete family Fi of closed subsets of there exists a pairwise disjoint family of open sets Ui, such that Fi ⊆ Ui. A family of subsets of is called discrete when every point of has a neighbourhood that intersects at most one of the sets from . An equivalent definition of collectionwise normal demands that the above Ui are themselves a discrete family, which is stronger than pairwise disjoint.
In mathematics, a content is a set function that is like a measure, but a content must only be finitely additive, whereas a measure must be countably additive. A content is a real function defined on a collection of subsets such that
In mathematics, the concept of a generalised metric is a generalisation of that of a metric, in which the distance is not a real number but taken from an arbitrary ordered field.
In mathematics, particularly measure theory, the essential range, or the set of essential values, of a function is intuitively the 'non-negligible' range of the function: It does not change between two functions that are equal almost everywhere. One way of thinking of the essential range of a function is the set on which the range of the function is 'concentrated'.
In topology and related areas of mathematics, a subset A of a topological space X is said to be dense in X if every point of X either belongs to A or else is arbitrarily "close" to a member of A — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it. Formally, is dense in if the smallest closed subset of containing is itself.
In mathematics, especially measure theory, a set function is a function whose domain is a family of subsets of some given set and that (usually) takes its values in the extended real number line which consists of the real numbers and










































