Regular space

Last updated
Separation axioms
in topological spaces
Kolmogorov classification
T0  (Kolmogorov)
T1  (Fréchet)
T2  (Hausdorff)
T2½ (Urysohn)
completely T2  (completely Hausdorff)
T3  (regular Hausdorff)
T3½ (Tychonoff)
T4  (normal Hausdorff)
T5  (completely normal
 Hausdorff)
T6  (perfectly normal
 Hausdorff)

In topology and related fields of mathematics, a topological space X is called a regular space if every closed subset C of X and a point p not contained in C have non-overlapping open neighborhoods. [1] Thus p and C can be separated by neighborhoods. This condition is known as Axiom T3. The term "T3 space" usually means "a regular Hausdorff space". These conditions are examples of separation axioms.

Contents

Definitions

The point x, represented by a dot on the left of the picture, and the closed set F, represented by a closed disk on the right of the picture, are separated by their neighbourhoods U and V, represented by larger open disks. The dot x has plenty of room to wiggle around the open disk U, and the closed disk F has plenty of room to wiggle around the open disk V, yet U and V do not touch each other. Regular space.svg
The point x, represented by a dot on the left of the picture, and the closed set F, represented by a closed disk on the right of the picture, are separated by their neighbourhoods U and V, represented by larger open disks. The dot x has plenty of room to wiggle around the open disk U, and the closed disk F has plenty of room to wiggle around the open disk V, yet U and V do not touch each other.

A topological space X is a regular space if, given any closed set F and any point x that does not belong to F, there exists a neighbourhood U of x and a neighbourhood V of F that are disjoint. Concisely put, it must be possible to separate x and F with disjoint neighborhoods.

A T3 space or regular Hausdorff space is a topological space that is both regular and a Hausdorff space. (A Hausdorff space or T2 space is a topological space in which any two distinct points are separated by neighbourhoods.) It turns out that a space is T3 if and only if it is both regular and T0. (A T0 or Kolmogorov space is a topological space in which any two distinct points are topologically distinguishable, i.e., for every pair of distinct points, at least one of them has an open neighborhood not containing the other.) Indeed, if a space is Hausdorff then it is T0, and each T0 regular space is Hausdorff: given two distinct points, at least one of them misses the closure of the other one, so (by regularity) there exist disjoint neighborhoods separating one point from (the closure of) the other.

Although the definitions presented here for "regular" and "T3" are not uncommon, there is significant variation in the literature: some authors switch the definitions of "regular" and "T3" as they are used here, or use both terms interchangeably. This article uses the term "regular" freely, but will usually say "regular Hausdorff", which is unambiguous, instead of the less precise "T3". For more on this issue, see History of the separation axioms.

A locally regular space is a topological space where every point has an open neighbourhood that is regular. Every regular space is locally regular, but the converse is not true. A classical example of a locally regular space that is not regular is the bug-eyed line.

Relationships to other separation axioms

A regular space is necessarily also preregular, i.e., any two topologically distinguishable points can be separated by neighbourhoods. Since a Hausdorff space is the same as a preregular T0 space, a regular space which is also T0 must be Hausdorff (and thus T3). In fact, a regular Hausdorff space satisfies the slightly stronger condition T2½. (However, such a space need not be completely Hausdorff.) Thus, the definition of T3 may cite T0, T1, or T2½ instead of T2 (Hausdorffness); all are equivalent in the context of regular spaces.

Speaking more theoretically, the conditions of regularity and T3-ness are related by Kolmogorov quotients. A space is regular if and only if its Kolmogorov quotient is T3; and, as mentioned, a space is T3 if and only if it's both regular and T0. Thus a regular space encountered in practice can usually be assumed to be T3, by replacing the space with its Kolmogorov quotient.

There are many results for topological spaces that hold for both regular and Hausdorff spaces. Most of the time, these results hold for all preregular spaces; they were listed for regular and Hausdorff spaces separately because the idea of preregular spaces came later. On the other hand, those results that are truly about regularity generally don't also apply to nonregular Hausdorff spaces.

There are many situations where another condition of topological spaces (such as normality, pseudonormality, paracompactness, or local compactness) will imply regularity if some weaker separation axiom, such as preregularity, is satisfied. [2] Such conditions often come in two versions: a regular version and a Hausdorff version. Although Hausdorff spaces aren't generally regular, a Hausdorff space that is also (say) locally compact will be regular, because any Hausdorff space is preregular. Thus from a certain point of view, regularity is not really the issue here, and we could impose a weaker condition instead to get the same result. However, definitions are usually still phrased in terms of regularity, since this condition is more well known than any weaker one.

Most topological spaces studied in mathematical analysis are regular; in fact, they are usually completely regular, which is a stronger condition. Regular spaces should also be contrasted with normal spaces.

Examples and nonexamples

A zero-dimensional space with respect to the small inductive dimension has a base consisting of clopen sets. Every such space is regular.

As described above, any completely regular space is regular, and any T0 space that is not Hausdorff (and hence not preregular) cannot be regular. Most examples of regular and nonregular spaces studied in mathematics may be found in those two articles. On the other hand, spaces that are regular but not completely regular, or preregular but not regular, are usually constructed only to provide counterexamples to conjectures, showing the boundaries of possible theorems. Of course, one can easily find regular spaces that are not T0, and thus not Hausdorff, such as an indiscrete space, but these examples provide more insight on the T0 axiom than on regularity. An example of a regular space that is not completely regular is the Tychonoff corkscrew.

Most interesting spaces in mathematics that are regular also satisfy some stronger condition. Thus, regular spaces are usually studied to find properties and theorems, such as the ones below, that are actually applied to completely regular spaces, typically in analysis.

There exist Hausdorff spaces that are not regular. An example is the set R with the topology generated by sets of the form U — C, where U is an open set in the usual sense, and C is a fixed nonclosed subset of R with empty interior.

Elementary properties

Suppose that X is a regular space. Then, given any point x and neighbourhood G of x, there is a closed neighbourhood E of x that is a subset of G. In fancier terms, the closed neighbourhoods of x form a local base at x. In fact, this property characterises regular spaces; if the closed neighbourhoods of each point in a topological space form a local base at that point, then the space must be regular.

Taking the interiors of these closed neighbourhoods, we see that the regular open sets form a base for the open sets of the regular space X. This property is actually weaker than regularity; a topological space whose regular open sets form a base is semiregular .

Related Research Articles

In topology and related branches of mathematics, a Hausdorff space ( HOWSS-dorf, HOWZ-dorf), separated space or T2 space is a topological space where, for any two distinct points, there exist neighbourhoods of each that are disjoint from each other. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" (T2) is the most frequently used and discussed. It implies the uniqueness of limits of sequences, nets, and filters.

In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces. These conditions are examples of separation axioms. A Tychonoff space is any completely regular space that is also a Hausdorff space; there exist completely regular spaces that are not Tychonoff.

This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space. These conditions are examples of separation axioms and their further strengthenings define completely normal Hausdorff spaces, or T5 spaces, and perfectly normal Hausdorff spaces, or T6 spaces.

In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which every point has a compact neighborhood.

In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space (named after Andrey Kolmogorov) if for every pair of distinct points of X, at least one of them has a neighborhood not containing the other. In a T0 space, all points are topologically distinguishable.

In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has a neighborhood not containing the other point. An R0 space is one in which this holds for every pair of topologically distinguishable points. The properties T1 and R0 are examples of separation axioms.

In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way: roughly speaking, neither overlapping nor touching. The notion of when two sets are separated or not is important both to the notion of connected spaces as well as to the separation axioms for topological spaces.

<span class="mw-page-title-main">General topology</span> Branch of topology

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology.

In topology, a discipline within mathematics, an Urysohn space, or T2½ space, is a topological space in which any two distinct points can be separated by closed neighborhoods. A completely Hausdorff space, or functionally Hausdorff space, is a topological space in which any two distinct points can be separated by a continuous function. These conditions are separation axioms that are somewhat stronger than the more familiar Hausdorff axiom T2.

In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such spaces are commonly called indiscrete, anti-discrete, concrete or codiscrete. Intuitively, this has the consequence that all points of the space are "lumped together" and cannot be distinguished by topological means. Every indiscrete space is a pseudometric space in which the distance between any two points is zero.

In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed. It is the smallest example of a topological space which is neither trivial nor discrete. It is named after Wacław Sierpiński.

In mathematics, a sober space is a topological space X such that every (nonempty) irreducible closed subset of X is the closure of exactly one point of X: that is, every irreducible closed subset has a unique generic point.

In topology and related areas of mathematics, a topological property or topological invariant is a property of a topological space that is invariant under homeomorphisms. Alternatively, a topological property is a proper class of topological spaces which is closed under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic to X possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets.

The history of the separation axioms in general topology has been convoluted, with many meanings competing for the same terms and many terms competing for the same concept.

In mathematics, the particular point topology is a topology where a set is open if it contains a particular point of the topological space. Formally, let X be any non-empty set and p ∈ X. The collection

In topology, two points of a topological space X are topologically indistinguishable if they have exactly the same neighborhoods. That is, if x and y are points in X, and Nx is the set of all neighborhoods that contain x, and Ny is the set of all neighborhoods that contain y, then x and y are "topologically indistinguishable" if and only if Nx = Ny. (See Hausdorff's axiomatic neighborhood systems.)

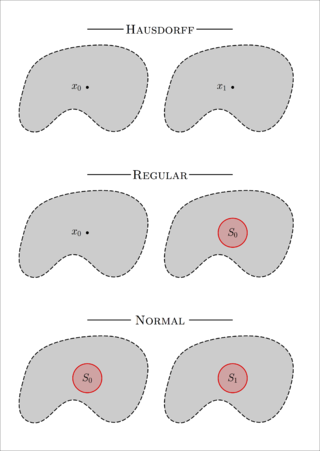
<span class="mw-page-title-main">Separation axiom</span> Axioms in topology defining notions of "separation"

In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms. These are sometimes called Tychonoff separation axioms, after Andrey Tychonoff.

References

  1. ↑ Munkres, James R. (2000). Topology (2nd ed.). Prentice Hall. ISBN   0-13-181629-2.
  2. ↑ "general topology - Preregular and locally compact implies regular". Mathematics Stack Exchange.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.